Arrumação de caixas
5 participantes
Página 1 de 2
Página 1 de 2 • 1, 2 
 Arrumação de caixas
Arrumação de caixas
Em uma das paredes de um depósito existem compartimentos de mesmo tamanho para armazenamento de caixas de dimensões frontais a e b. A terceita dimensão da caixa coincide com a profundidade de cada um dos compartimentos . Inicialmente as caixas são arrumadas, em cada um deles, como representado na Figura 1. A fim de aproveitar melhor o espaço, uma nova proposta de disposição das caixas foi idealizada e está indicada na Figura 2. Essa nova proposta possibilitaria o aumento do número de caixas armazenadas de 10 para 12 e a eliminação de folgas.

É possível ocorrer a troca de arrumação segundo a nova proposta?
a) Não, porque a segunda proposta deixa uma folga de 4 cm na altura do compartimento, que é de 12 cm, o que permitria colocar um número maior de caixas.
b) Não, porque, para aceitar a segunda proposta, seria necessário praticamente dobrar a altura e reduzir à metade a largura do compartimento.
c) Sim, porque a nova disposição das caixas ficaria acomodada perfeitamente no compartimento de 20 cm de altura por 27 cm de largura.
d) Sim, pois efetivamente aumentaria o número de caixas e reduziria o número de folgas para apenas uma de 2 cm na largura do comprimento.
e) Sim, porque a nova disposição de caixas ficaria acomodada perfeitamente no compartimento de 32 cm de altura por 45cm de largura.

É possível ocorrer a troca de arrumação segundo a nova proposta?
a) Não, porque a segunda proposta deixa uma folga de 4 cm na altura do compartimento, que é de 12 cm, o que permitria colocar um número maior de caixas.
b) Não, porque, para aceitar a segunda proposta, seria necessário praticamente dobrar a altura e reduzir à metade a largura do compartimento.
c) Sim, porque a nova disposição das caixas ficaria acomodada perfeitamente no compartimento de 20 cm de altura por 27 cm de largura.
d) Sim, pois efetivamente aumentaria o número de caixas e reduziria o número de folgas para apenas uma de 2 cm na largura do comprimento.
e) Sim, porque a nova disposição de caixas ficaria acomodada perfeitamente no compartimento de 32 cm de altura por 45cm de largura.

joaocarvalho- Padawan

- Mensagens : 57
Data de inscrição : 23/01/2013
Idade : 32
Localização : Recife Pernambuco Brasil
 Re: Arrumação de caixas
Re: Arrumação de caixas
Sejam H e L a altura e a largura do compartimento
1ª figura ----> H = 2b + 2 ----> L = 5a + 5
2ª figura ----> H = 4a ----> L = 3b
Igualando H ---> 4a = 2b + 2 ---> 2a = b + 1 ---> *5 ---> 10a = 5b + 5 ---> I
Igualando L ---> 3b = 5a + 5 ---> 5a = 3b - 5 ---> *2 ---> 10a = 6b - 10 ---> II
II = I ----> 6b - 10 = 5b = 5 ---> b = 15 ----> a = 8
H = 4a ---> H = 4.8 ----> H = 32
L = 3b ---> L = 3.15 ----> L = 45
Alternativa E
1ª figura ----> H = 2b + 2 ----> L = 5a + 5
2ª figura ----> H = 4a ----> L = 3b
Igualando H ---> 4a = 2b + 2 ---> 2a = b + 1 ---> *5 ---> 10a = 5b + 5 ---> I
Igualando L ---> 3b = 5a + 5 ---> 5a = 3b - 5 ---> *2 ---> 10a = 6b - 10 ---> II
II = I ----> 6b - 10 = 5b = 5 ---> b = 15 ----> a = 8
H = 4a ---> H = 4.8 ----> H = 32
L = 3b ---> L = 3.15 ----> L = 45
Alternativa E

Elcioschin- Grande Mestre

- Mensagens : 73186
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Arrumação de caixas
Re: Arrumação de caixas
[img]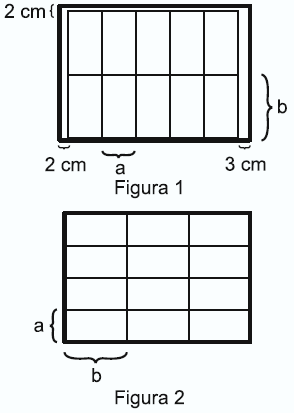 [/img]
[/img]
Mestre, não entendi uma coisa: por que o senhor igualou as medidas?
Tudo bem que isso serve para descobrir a e b, MAS isso só seria possível se a disposição IDEALIZADA coincidisse com a resposta.
O que eu acho que poderia dar errado, SE a resposta fosse "Não" (letras A e B).
Corrija-me se eu estiver errado. Obg!
 [/img]
[/img]Mestre, não entendi uma coisa: por que o senhor igualou as medidas?
Tudo bem que isso serve para descobrir a e b, MAS isso só seria possível se a disposição IDEALIZADA coincidisse com a resposta.
O que eu acho que poderia dar errado, SE a resposta fosse "Não" (letras A e B).
Corrija-me se eu estiver errado. Obg!

Gustavoadp- Estrela Dourada

- Mensagens : 1036
Data de inscrição : 05/07/2014
Idade : 27
Localização : Recife, PE
 Re: Arrumação de caixas
Re: Arrumação de caixas
Porque o compartimento não mudou de tamanho 45x32 e 32x45: ele mudou apenas de posição ---> em pé para deitado
Inverteu-se apenas caixas em pé (8x15) para caixas deitadas (15x8).
Inverteu-se apenas caixas em pé (8x15) para caixas deitadas (15x8).

Elcioschin- Grande Mestre

- Mensagens : 73186
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Arrumação de caixas
Re: Arrumação de caixas
Mas na parte deitada tem 2 caixas a mais

Gustavoadp- Estrela Dourada

- Mensagens : 1036
Data de inscrição : 05/07/2014
Idade : 27
Localização : Recife, PE
 Re: Arrumação de caixas
Re: Arrumação de caixas
Exatamente: e o enunciado afirmou que isto acontece:
" Essa nova proposta possibilitaria o aumento do número de caixas armazenadas de 10 para 12 e a eliminação de folgas."
Uma simples mudança na posição do compartimento possibilitou armazenar mais duas caixas!
E alternativa E diz exatamente isto!
" Essa nova proposta possibilitaria o aumento do número de caixas armazenadas de 10 para 12 e a eliminação de folgas."
Uma simples mudança na posição do compartimento possibilitou armazenar mais duas caixas!
E alternativa E diz exatamente isto!

Elcioschin- Grande Mestre

- Mensagens : 73186
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Arrumação de caixas
Re: Arrumação de caixas
Por que 2b+1? Não seria 2b+2?
Papaleguas- Iniciante
- Mensagens : 5
Data de inscrição : 23/02/2016
Idade : 26
Localização : Curitiba,Paraná,Brasil
 Re: Arrumação de caixas
Re: Arrumação de caixas
A equação é: 4a = 2b + 2
Dividindo por 2: 2a = b + 1
Dividindo por 2: 2a = b + 1

Elcioschin- Grande Mestre

- Mensagens : 73186
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Arrumação de caixas
Re: Arrumação de caixas
Ah... obrigado Grande Mestre!
Papaleguas- Iniciante
- Mensagens : 5
Data de inscrição : 23/02/2016
Idade : 26
Localização : Curitiba,Paraná,Brasil
 Re: Arrumação de caixas
Re: Arrumação de caixas
A resposta só é possível se vc partir já desde o início que a arrumação foi possível. Não dá para simplesmente descobrir que ela foi possível. Questão mal feita.
diegpl- Iniciante
- Mensagens : 36
Data de inscrição : 20/11/2015
Idade : 36
Localização : Ipatinga
Craftmir2003 gosta desta mensagem
Página 1 de 2 • 1, 2 
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos












