Momento Linear 2!

Uma espingarda de mola possui massa desprezível e a constante da mola é dada por k=400 N/m. A mola é comprimida 6,0 cm e uma bala de massa 0,0300 kg é colocada no cano horizontal contra a mola comprimida. A seguir, a mola é liberada e a bala recebe um impulso, saindo do cano da arma. O cano possui 6,0 cm de comprimento, de modo que a bala deixa o cano no mesmo ponto onde ela perde o contato com a mola. A arma é mantida de modo que o cano fique na horizontal.

a) Desprezando o atrito, calcule a velocidade da bala ao deixar o cano da arma.
b) Calcule a velocidade com que a bala deixa o cano da arma quando uma força resistiva constante de 6,00 N age sobre ela enquanto ela se move ao longo do cano.
c) Para a sistuação descrita no item (b), em que posição ao longo do cano a bala possui sua velocidade máxima e qual é essa velocidade?

Esse problema envolve energia. Comecemos:

Letra A)
Podemos dizer que toda a energia armazenada pela mola será transformada em energia cinética. Ou seja, temos energia potencial elástica tornando-se energia cinética. A equação é a seguinte:




Substituindo os valores:




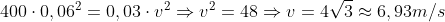
Letra B)
O raciocínio será o mesmo, mas agora teremos uma força oposta. Essa força realizará um trabalho dado por:

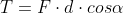
Alpha é o ângulo entre a força e o deslocamento. Esse ângulo vale 180°, como cos 180° = -1, temos:



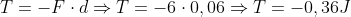
Vamos montar a equação:


Agora, vamos substituir:



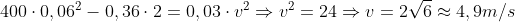
Letra C
Acredito que a resposta será a mesma da letra B. Com velocidade aprox = 4,9 m/s e no fim do cano (após percorrer 6cm).
Veremos o porquê, rearranjando uma expressão já definida:




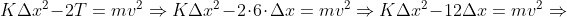
Agora vamos substituir o que temos e ficaremos com uma função da velocidade em função do deslocamento:




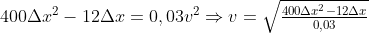
Essa função, para valores positivos de X, retornará (nos reais) valores positivos de Y, formando uma reta, o que é possível verificar na representação do gráfico, no link abaixo:
http://www.wolframalpha.com/input/?i=input+sqrt%28%28400*x%5E2%29-%2812*x%29%29%2Fsqrt%280.03%29


Assim, o maior valor de V, vem com o maior valor de X possível. Sabemos que o maior valor de X possível é quando a bala chega ao fim da mola, X=0,06. Substituindo na função, virá v = 4,9 m/s (aprox).


Abraço, qualquer coisa posta!

Editei minha resolução acima, agora com a letra C.... dê uma olhada!

gabrielferreira95 Como vc encontra esse DeltaX nas equações?

A equação da energia potencial elástica: (K∆x^2) / 2... a partir dela desenvolvi outras expressões como descrito na resolução.

Meu o que deu errado no meu raciocínio da B)

FR=Fe-Fr
FR=400*0,06-6=18N

T=F*d
T=1,08J

T=Ec
1,08=0,03*v²/2
v=8,5m/s

o pior que nâo vejo erro!

Thiago ro,nesse caso voce deve usar a expressao da energia potencial elastica. da forma como voce fez está errado. Veja:
Você calculou a forca exercida pela mola quando esta estava completamente pressionada: 400*0,06 ...no entanto, essa forca não é constante ao longo do percurso porque o estiramento vai diminuindo. por isso você não pode escrever T = F*d... Assumindo que F é constante ao longo dos 6 cm... Pois NÃO é constante.

Como então calcular o trabalho exercido pela mola? Usando a equacao da energia potencial elástica.

Ou então, você pode fazer o seguinte raciocínio. Construa um gráfico da forca elástica em função do estiramento da mola. Um grafico de força versus distancia, (N x m). A força vai variar um certo valor F, além de o estiramento variar um certo valor x. Concorda que a figura formada é um triângulo? A área do triângulo eqüivale ao trabalho da forca elástica. A área e dada por F x /2 = kxx/2 = kx^2/2 = T, que eqüivale exatamente a equação da energia potencial elástica.

Entendeu?