(Mackenzie 98) - Equações modulares

por carlos.r Sáb 16 Mar 2013, 11:20

(Mackenzie 98) Analisando graficamente as funções (I), (II), (III) e (IV) a seguir.

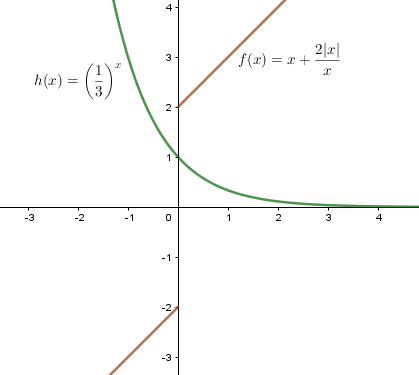
I) f(x) = x + (2|x|)/x de IR* em IR.
II) g(x) = 3x - x³ de [-√3, √3] em [-2, 2]
Obs.: g (-1) é mínimo.
III) h(x) = (1/3)^x de IR em IR* - {0}.
IV) t(x) = 3, de IR em {3}.

O número de soluções reais da equação h(x) = f(x) é:

a) 0
b) 1
c) 2
d) 3
e) 4

Spoiler:

Ajuda, por favor. Obrigado.

por Luck Sáb 16 Mar 2013, 14:52

h(x) = f(x)
(1/3)^x = x + (2|x|)/x
para x >0: (1/3)^x = x + 2 , e para x < 0 :(1/3)^x = x - 2
com isso faça o esboço do gráfico e verá que a função f(x) e h(x) nao se cortam, logo nao há solução, letra a.

por **Emanoel Mendonça** Ter 23 Out 2018, 21:49

Não entendi muito bem a solução do Luck, alguém pode trocar em miúdos pra mim ?? Grato desde já

por **Giovana Martins** Ter 23 Out 2018, 22:06

Veja se dá para entender. Do contrário, avise-me.

(Mackenzie 98) - Equações modulares Screen52

\\|x|=x,se\ x> 0\ \vee\ |x|=-x,se\ x<0\\\\x> 0:\ f(x)=x+\frac{2|x|}{x}=x+\frac{2x}{x}=x+2\\\\x<0:\ f(x)=x+\frac{2|x|}{x}=x+\frac{2(-x)}{x}=x-2\\\\\therefore \ f(x)=x+2,se\ x>0\ \vee\ f(x)=x-2,se\ x<0\\\\\therefore \ x>0:\ f(x)=h(x)\rightarrow x+2=\left ( \frac{1}{3} \right )^x\\\\\therefore \ x<0:\ f(x)=h(x)\to x-2=\left ( \frac{1}{3} \right )^x

Nota: por definição |x|=x, se x ≥ 0 v |x|=-x, se x < 0, entretanto, temos que modificar a definição para não cairmos em uma divisão por zero.