AFA 2001
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
AFA 2001
por AFA 2013 Dom 24 Fev 2013, 09:36
Considere no campo complexo uma curva tal que Im(2/z)≥ k, onde z é um complexo não nulo. Se k=2, tem-se sua representação gráfica dada pelo
a) círculo de raio 1/4 e tangente ao eixo real.
b) círculo de raio 1/2 e tangente ao eixo imaginário.
c) conjunto de pontos do plano complexo exterior ao círculo de raio 1/2 e centro (-1/2,0)
d) círculo de raio 1/2 e tangente ao eixo real.
Resposta:d
a) círculo de raio 1/4 e tangente ao eixo real.
b) círculo de raio 1/2 e tangente ao eixo imaginário.
c) conjunto de pontos do plano complexo exterior ao círculo de raio 1/2 e centro (-1/2,0)
d) círculo de raio 1/2 e tangente ao eixo real.
Resposta:d
AFA 2013- Iniciante
- Mensagens : 26
Data de inscrição : 01/02/2013
Idade : 30
Localização : Minas Gerais
Re: AFA 2001
por NiltonGMJunior Dom 24 Fev 2013, 11:29
Façamos:
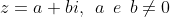
Temos que:
}{a^2+b^2}=\frac{2a-2b}{a^2+b^2}=\frac{2a}{a^2+b^2}-\frac{2bi}{a^2+b^2} "\frac{2}{z}=\frac{2}{a+bi}=\frac{2(a-bi)}{a^2+b^2}=\frac{2a-2b}{a^2+b^2}=\frac{2a}{a^2+b^2}-\frac{2bi}{a^2+b^2}")
Portanto:
=\frac{-2bi}{a^2+b^2} "Im(\frac{2}{z})=\frac{-2bi}{a^2+b^2}")
Logo, como k=2:
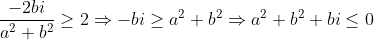
Lembre-se que a equação normal de uma cicunferência é:
Em que x0 e y0 representam as coordenadas de um ponto da circunferência e r representa o raio.
Perceba que nosso a e nosso b correspondem, respectivamente, ao x e y no plano cartesiano, e o i (unidade imaginária) equivale a uma unidade no eixo das ordenadas, portanto essa é nossa equação:
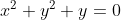
Para encontrar a coordenada do centro da circunferência basta dividir os termos que multiplicam x e y por -2, lembre-se desse macete. Portanto como o termo que acompanha o x é igual a 0 e o termo que acompanha o y é igual a 1, temos que o centro de nossa circunferência é:
 \rightarrow C(0;\frac{-1}{2}) "C(\frac{0}{-2};\frac{1}{-2}) \rightarrow C(0;\frac{-1}{2})")
O raio da circunferência é dado por:
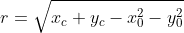
Em que xC e yC representam as coordenadas do centro e x0 e y0 os termos independentes de x e y na equação da circunferência, portanto como nosso xC = 0, yC = -1/2, x0 = 0 e y0 = 0, temos que:
^2}=\frac{1}{2} "r=\sqrt{\left \(\frac{-1}{2}\right \)^2}=\frac{1}{2}")
Temos entãouma circunferência de Centro C(0,-1/2) e raio r=1/2, fazendo o gráfico:
Considerando que o eixo das abcissas corresponde ao eixo dos reais e o o eixo das ordenadas corresponde ao eixo dos imaginários temos o gráfico de um círculo de raio 1/2 que tangencia o eixo real.
Alternativa D
Temos que:
Portanto:
Logo, como k=2:
Lembre-se que a equação normal de uma cicunferência é:
Em que x0 e y0 representam as coordenadas de um ponto da circunferência e r representa o raio.
Perceba que nosso a e nosso b correspondem, respectivamente, ao x e y no plano cartesiano, e o i (unidade imaginária) equivale a uma unidade no eixo das ordenadas, portanto essa é nossa equação:
Para encontrar a coordenada do centro da circunferência basta dividir os termos que multiplicam x e y por -2, lembre-se desse macete. Portanto como o termo que acompanha o x é igual a 0 e o termo que acompanha o y é igual a 1, temos que o centro de nossa circunferência é:
O raio da circunferência é dado por:
Em que xC e yC representam as coordenadas do centro e x0 e y0 os termos independentes de x e y na equação da circunferência, portanto como nosso xC = 0, yC = -1/2, x0 = 0 e y0 = 0, temos que:
Temos entãouma circunferência de Centro C(0,-1/2) e raio r=1/2, fazendo o gráfico:
Considerando que o eixo das abcissas corresponde ao eixo dos reais e o o eixo das ordenadas corresponde ao eixo dos imaginários temos o gráfico de um círculo de raio 1/2 que tangencia o eixo real.
Alternativa D
NiltonGMJunior- Padawan
- Mensagens : 50
Data de inscrição : 28/10/2012
Idade : 29
Localização : São Paulo - SP, Brasil
Emilyvq gosta desta mensagem
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
