UFMS geometria plana

por rafael_dark Sáb 23 Fev 2013, 16:07

Três círculos C1, C2 E C3, são tangentes a uma reta t, conforme ilustra a figura abaixo. O raio de C1 mede 40cm, o de C2 mede 90 cm e o de C3 mede r cm. Sabendo que os três círculos são tangentes entre si, determine 10r ( resposta 144 ) Desde já agradeço

UFMS geometria plana Image011

por **raimundo pereira** Sáb 23 Fev 2013, 23:15

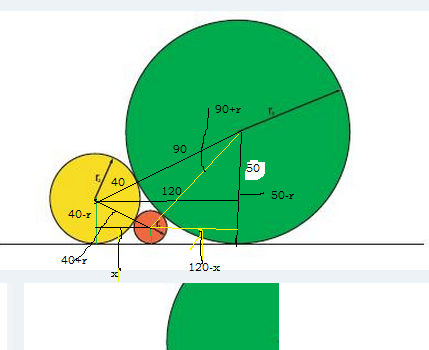
Vou mostrar um caminho , faça as contas e veja se chega ao gabarito.

trabalhe com os triângulos retângulos de catetos:(Pitágoras)
1 - 40-r,x e hipotenusa 40+r
2 - 120-x,50-r e hipotenusa 90+r
3 - ache os valores de x em função de r . Iguale os valores de x para achar r.
Boa Noite

att

por Irineu Shimabukuro Qui 31 Dez 2015, 17:41

Entendi a resolução. Porém é 90-r ,em vez de 50-r.

por JohnnyC Sex 06 Ago 2021, 03:04

pessoal, alguém poderia verificar essa questão ? eu consegui compreender a resolução do Raimundo, porém, ao botarmos no papel, a gente continua a achar r em função de x.
A resposta é 144 cm.

ps: no item 3 do raimundo o correto é: r + 90 (hipotenusa), 120 - x e 90 - r como catetos.

por **tales amaral** Sex 06 Ago 2021, 10:40

JohnnyC escreveu:pessoal, alguém poderia verificar essa questão ? eu consegui compreender a resolução do Raimundo, porém, ao botarmos no papel, a gente continua a achar r em função de x.
A resposta é 144 cm.

ps: no item 3 do raimundo o correto é: r + 90 (hipotenusa), 120 - x e 90 - r como catetos.

Temos 2 triângulos retângulos:

Um com lados (90+r,90-r,120-x) e outro com lados (40+r,40-r,x). Montando um sistema:

[latex]\begin{cases} (90+r)^2 = (90-r)^2+(120-x)^2\\~\\ (40+r)^2 = (40-r)^2+x^2 \end{cases}[/latex]

Resolvendo o sistema, dá r = 72/5 = 14.4 -> 10r = 144.

(Para resolver o sistema, eu abusei do [latex]a^2-b^2 = (a+b)(a-b)[/latex])