Área de setor circular - Mackenzie 2000

por tiagopw Sex 23 Nov 2012, 19:41

Determinar a área do setor assinalado no círculo de raio 1 e centro O.

Área de setor circular - Mackenzie 2000 NbBdPLf30F4+trXvww8Wj1C9KYLHkUs2BclK5XA5MDm0YigdtHopfBFNUiTVSnRAoSKyEQEFiJQQKEishUJBY6RUowAoS0qkCQl6CgoTErP8H5ESw5CEN7rcAAAAASUVORK5CYII=

Área de setor circular - Mackenzie 2000 NbBdPLf30F4+trXvww8Wj1C9KYLHkUs2BclK5XA5MDm0YigdtHopfBFNUiTVSnRAoSKyEQEFiJQQKEishUJBY6RUowAoS0qkCQl6CgoTErP8H5ESw5CEN7rcAAAAASUVORK5CYII=

R - 7pi / 18

Agradeço o apoio!

Paz e luz!

por **Leonardo Sueiro** Sex 23 Nov 2012, 19:51

É uma potência de ponto
O ângulo oposto ao ângulo central correspondente ao ângulo de 110º vale:

360 - 2.110 = 140º

360 ---> pi1^2
140 ---> x

x = 140pi/360

x = 7pi/18

por **Leonardo Sueiro** Sex 23 Nov 2012, 19:54

Na verdade, acho que não é um caso de "potência de ponto". Se não me engano, potência de ponto envolve medidas de comprimento apenas

Mas o nome pouco importa. O importante é saber que o ângulo inscrito é metade do central correspondente

por Glauber Damasceno Sex 23 Nov 2012, 19:55

O arco que o ângulo inscrito 110º enxerga vale seu dobro : 220º
Logo o que sobra é a medida do arco o qual o ângulo central O enxerga
Ângulo central = 140º

Área do setor circular : ∏R²α/360

=∏ 1².140/360 = 7∏/18

por Glauber Damasceno Sex 23 Nov 2012, 19:58

Postaste mais rápido que eu , camarada leosueiro123 .
Aproveitando sua presença por aqui , teria como analisar minha questão ?
Desde já grato.

por **Leonardo Sueiro** Sex 23 Nov 2012, 20:01

Vou ver se a encontro

por tiagopw Sex 23 Nov 2012, 20:10

Obrigado pelo apoio pessoal, acho q estou cansado de estudar por hoje, pois depois da explicação é que enxerguei a propriedade!

Abs e um bom fds!

por **raimundo pereira** Sex 23 Nov 2012, 20:41

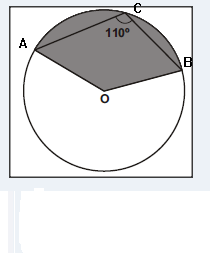
Área de setor circular - Mackenzie 2000 2mg9w0l

Outro modo:

Ângulo inscrito A^CB=110º --->Arco AB = 110.2=220º
Ângulo central AOB = θ = 360-220 = θ= 140º
Área do setor circular AOB S=θ . R²/2, sendo θ em radianos.
Transformando 140º em radianos, temos
180º ----- pi rad
140º ----- x rad
x = 7pi/9

S = θ.1²/2 ---> S = 7pi/18

por **Leonardo Sueiro** Sex 23 Nov 2012, 20:48

Foi o que nós fizemos, Raimundo

por **raimundo pereira** Sex 23 Nov 2012, 21:09

Desculpem-me , infelizmente não vi a resolução do Glauber , somente a sua e achei melhor mostrar outra o opção para o Thiago, revisando os conceitos de ângulo inscrito, ângulo central e área do setor.

att