Determinante (Pucpr)

por Hunter_LeoHenriques Ter 23 Out - 21:23

Gostaria de uma ajuda nessa questão, contando com a resolução para que assim possa aprender a resolve-lá
Ela envolve determinante e adquiri-lá pelo site: diadematematica.com/modules/myiframe/index.php?iframeid=92
Obrigado pela ajuda

(Pucpr) A soma dos valores de Y para que a det( A + YI ) = 0, onde I é matriz identidade, é:

A= [ 4 2 1 ]
[ -2 0 -1]
[ 2 2 3]

obs.: A é uma matriz 3x3, não consegui adicionar a imagem
espero que consigam entender ou acessar o link acima para conferirem qualquer dúvida..
Mesmo assim, muito obrigado

por **JoaoGabriel** Ter 23 Out - 21:49

É dado que det(A + yI) = 0. Temos informações de A. Façamos yI:

$\\yI\to y\times\begin{pmatrix} 1 & 0 & 0\\ 0&1 &0 \\ 0&0 &1 \end{pmatrix}=\begin{pmatrix} y & 0 & 0\\ 0& y & 0\\ 0&0 & y \end{pmatrix}$

Façamos A +yI:

$\\\begin{pmatrix} y & 0 & 0\\ 0& y & 0\\ 0&0 & y \end{pmatrix}+\begin{pmatrix} 4 & 2&1 \\ -2 & 0 &-1 \\ 2&2 &3 \end{pmatrix}=\begin{pmatrix} 4+y &2 &1 \\ -2& y &-1 \\ 2 &2 & 3+y \end{pmatrix}$

A partir de agora é com você: calcule este determinante por Sarrus ou Laplace e iguale a zero, depois faça a soma dos valores de y!

Se não sair é só falar que nós vemos, abraços

por Hunter_LeoHenriques Ter 23 Out - 22:09

Hahahah.. agora ficou fácil, muito obrigado mesmo, tanto pela atenção quanto pela ajuda, o restante eu resolvo sim... Um grande abraço também e parabéns pela dedicação e ajuda!

por Hunter_LeoHenriques Ter 23 Out - 23:10

Olha só João Gabriel eu tive problemas com a resolução da equação de terceiro grau formada na determinante, tem como dar uma olhadinha a respeito dela para mim???

por **Robson Jr.** Ter 23 Out - 23:36

Você não precisa resolver a equação para encontrar a soma das raízes. Use as relações de Girard.

por Hunter_LeoHenriques Ter 23 Out - 23:40

Robson Jr. escreveu:Você não precisa resolver a equação para encontrar a soma das raízes. Use as relações de Girard.

Não entendi muito bem, como ficaria essa relação aplicada a equação, só para ter como exemplo

por **Robson Jr.** Ter 23 Out - 23:50

Vou usar como exemplo um polinômio genérico do grau 3:

$p(x)=ax^3+bx^2+cx+d$

Das relações de Girard, a soma das raízes desse polinômio vale:

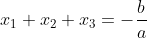
$x_1+x_2+x_3=-\frac{b}{a}$

Girard é um dos assuntos mais importantes estudados na teoria de polinômios.