Área do quadrado

por luizdaniel Dom 23 Set 2012, 11:44

Seja P um ponto do interior de um quadrado tal que as distâncias a três de seus vértices consecutivos sejam iguais a 1, 4 e 5, nesta ordem. A área deste quadrado é igual a?

Resposta: 17

por Paracampos Sáb 29 Set 2012, 04:14

imageshack.us/photo/my-images/844/exercicio.png/

Ligando o ponto aos vértices obtemos um angulo de 90 °
e assim podemos usar pitágoras.

1² + 4² = a²
a² = 1 + 16
a² = 17
a = Raiz de 17

após acharmos o valor do lado, achamos a area que é
a.a = raiz de 17 vezes raiz de 17 = 17

Espero ter ajudado

por **Medeiros** Dom 30 Set 2012, 01:17

Este exercício é muito chato, praticamente não tem geometria, só álgebra e conta. Mas vamos lá.

Seja o quadrado ABCD de aresta a e ponto interno P, onde considero os ângulos u, v e w assinalados na figura.

Pela lei dos cossenos aplicada aos triângulos:

∆APC -----> (a√2)² = 1² + 5² - 2.1.5.cos(u) -----> cos(u) = (13-a²)/5

∆APB -----> a² = 1² + 4² - 2.1.4.cos(v) -----> cos(v) = (17-a²)/8

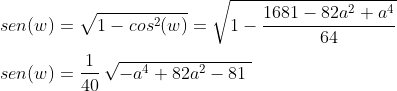
$Área do quadrado Gif$

∆BPC -----> a² = 4² + 5² - 2.4.5.cos(w) -----> cos(w) = (41-a²)/40

$Área do quadrado Gif$

mas
u = v + w ----> cos(u) = cos(v+w)
então
cos(u) = cos(v).cos(w) - sen(v).sen(w)

substituindo os valores encontrados acima,

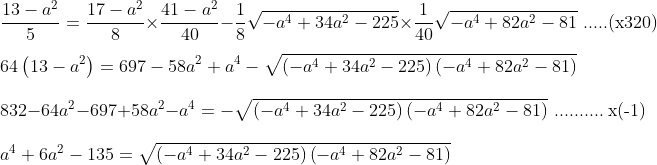
$Área do quadrado Gif.latex?%5C%5C%20%5Cfrac%7B13-a%5E2%7D%7B5%7D=%5Cfrac%7B17-a%5E2%7D%7B8%7D%5Ctimes%20%5Cfrac%7B41-a%5E2%7D%7B40%7D-%5Cfrac%7B1%7D%7B8%7D%5Csqrt%7B-a%5E4+34a%5E2-225%7D%5Ctimes%20%5Cfrac%7B1%7D%7B40%7D%5Csqrt%7B-a%5E4+82a%5E2-81%7D%5Ctext%7B%20.....%28x320%29%7D%5C%5C%5C%5C%2064%5Cleft%2813-a%5E2%20%5Cright%20%29=697-58a%5E2+a%5E4-%5Csqrt%7B%5Cleft%28-a%5E4+34a%5E2-225%20%5Cright%20%29%5Cleft%28%20-a%5E4+82a%5E2-81%5Cright%20%29%7D%5C%5C%5C%5C%20832-64a%5E2-697+58a%5E2-a%5E4=-%5Csqrt%7B%5Cleft%28-a%5E4+34a%5E2-225%20%5Cright%20%29%5Cleft%28%20-a%5E4+82a%5E2-81%5Cright%20%29%7D%5Ctext%7B%20.........$

fazendo, para simplificar as contas: a²=t
e elevando ao quadrado os dois membros, temos:

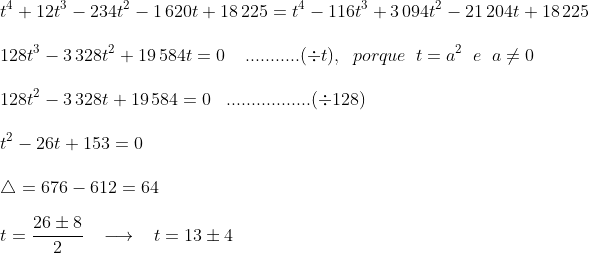
$Área do quadrado Gif.latex?%5C%5C%20t%5E4+12t%5E3-234t%5E2-1%5C,620t+18%5C,225=t%5E4-116t%5E3+3%5C,094t%5E2-21%5C,204t+18%5C,225%20%5C%5C%5C%5C%20128t%5E3-3%5C,328t%5E2+19%5C,584t=0%20%5C;%5C;%5C;%5C;%5Ctext%7B...........%7D%28%5Cdiv%20t%29,%5C;%5C;porque%5C;%5C;t=a%5E2%5C;%5C;e%5C;%5C;a%5Cneq%200%5C%5C%5C%5C%20128t%5E2-3%5C,328t+19%5C,584=0%5C;%5C;%5C;%5Ctext%7B................$

hipóteses

1) para t=9 ---> a²=9 ---> a=3 ⇒ diagonal = 3√2 ≈ 4,2 ----> NÃO SERVE pois segmento CP=5 não cabe dentro do quadrado.

2) para t=17 ---> a²=17 ---> a=√17 ⇒ diagonal =√17.√2=√34 ≈ 5,83 > 5 ----> SERVE

portanto: S = a² = 17

Percebemos, agora, que v é um ângulo reto pois cos(v)=(17-17)/8=0 ⇒ v=90º ou v=270º (não faz sentido)