vértices do quadrado
3 participantes
Página 1 de 1
 vértices do quadrado
vértices do quadrado
Dados dois vértices consecutivos A(2;0) e B(-1;4) de um quadrado, determinar as equações das retas que contém os seus lados.
resposta:de um deles: 4x+3y-8=0; 4x+3Y+17=0; 3x-4y-6=0; 3x-4y+19=0
do outro: 4x+3y-8=0; 4x+3y-33=0; 3x-4y-6=0; 3x-4y+19=0
resposta:de um deles: 4x+3y-8=0; 4x+3Y+17=0; 3x-4y-6=0; 3x-4y+19=0
do outro: 4x+3y-8=0; 4x+3y-33=0; 3x-4y-6=0; 3x-4y+19=0

jessicajessica- Jedi

- Mensagens : 418
Data de inscrição : 18/05/2012
Idade : 29
Localização : Arujá, SP
 Re: vértices do quadrado
Re: vértices do quadrado
Oi!
Veja o a imagem:

Perceba que AB//DC e BD//AC
A coordenada dos pontos A(2,0) e B(-1,4) nos permite encontrar o coeficiente angular que é -4/3.
Como a figura é um quadrado, a reta AB é perpendicular a BD e a AC. Logo, o coeficiente mAB.mBD = -1
Concluimos, portanto, que mBD = mAC = 3/4
e mBA = mDC = -4/3 (retas paralelas possuem o mesmo coeficiente angular, lembra?)
Para acharmos as coordenadas do ponto C eu fiz uma semelhança de triângulos. Veja que na direita temos o triangulo 3,4 e 5. Pelo uso de ângulos genéricos alpha e beta, achei outro triangulo em que a hipotenusa é AC. Para descobrir que eles são semelhantes, basta ver que alpha + 90 é o angulo externo do triângulo a direita, Sendo assim, encontramos um triangulo semelhante de mesmas medidas 3,4 e 5 logo abaixo do quadrado. Pela medidas dos catetos, conclui-se que as coordenadas do ponto C(6,3).
Agora que você sabe as coordenadas de 3 pontos, pode aplicar a equação da reta para as três arestas: y-yo= m(x-xo)
Para a reta AB, use mAB e o ponto A ou B
Para a reta AC, use mAC e o ponto A ou C
Para a reta BD, use mBD e o ponto B
Para a reta DC, use mDC e o ponto C
Chega-se a segunda resposta. Qualquer dúvida, só perguntar
Veja o a imagem:

Perceba que AB//DC e BD//AC
A coordenada dos pontos A(2,0) e B(-1,4) nos permite encontrar o coeficiente angular que é -4/3.
Como a figura é um quadrado, a reta AB é perpendicular a BD e a AC. Logo, o coeficiente mAB.mBD = -1
Concluimos, portanto, que mBD = mAC = 3/4
e mBA = mDC = -4/3 (retas paralelas possuem o mesmo coeficiente angular, lembra?)
Para acharmos as coordenadas do ponto C eu fiz uma semelhança de triângulos. Veja que na direita temos o triangulo 3,4 e 5. Pelo uso de ângulos genéricos alpha e beta, achei outro triangulo em que a hipotenusa é AC. Para descobrir que eles são semelhantes, basta ver que alpha + 90 é o angulo externo do triângulo a direita, Sendo assim, encontramos um triangulo semelhante de mesmas medidas 3,4 e 5 logo abaixo do quadrado. Pela medidas dos catetos, conclui-se que as coordenadas do ponto C(6,3).
Agora que você sabe as coordenadas de 3 pontos, pode aplicar a equação da reta para as três arestas: y-yo= m(x-xo)
Para a reta AB, use mAB e o ponto A ou B
Para a reta AC, use mAC e o ponto A ou C
Para a reta BD, use mBD e o ponto B
Para a reta DC, use mDC e o ponto C
Chega-se a segunda resposta. Qualquer dúvida, só perguntar

Giiovanna- Grupo
Velhos amigos do Fórum
- Mensagens : 2128
Data de inscrição : 31/08/2012
Idade : 30
Localização : São Paulo, SP
 Re: vértices do quadrado
Re: vértices do quadrado
Olá!
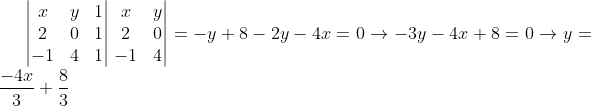
Sendo esta a equação da reta AB, e tendo coeficiente angular igual a:m=-4/3.
A reta BC é perpendicular a reta AB,portanto ela tem coeficiente angular igual a:
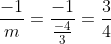
O ponto B(-1,4), pertence a reta BC portanto.
\rightarrow y-4=\frac{3}{4}(x+1)\rightarrow y=\frac{3x}{4}+\frac{19}{4})
O ponto C vai ter como coordenadas.
(x,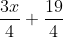 )
)
Encontramos agora a medida do lado do quadrado.
^{2}+(4)^{2}}\rightarrow d=5)
Encontramos assim o valor de x.
^{2}+\left ( \frac{3x}{4}+\frac{19}{4}-4 \right )^{2}\rightarrow 25=x^{2}+2x+1+\frac{9x^{2}}{16}+\frac{18x}{16}+\frac{9}{16}\rightarrow 25=\frac{25x^{2}}{16}+\frac{50x}{16}+\frac{25}{16}\rightarrow 400=25x^{2}+50x+25\rightarrow 25x^{2}+50x-375\rightarrow x^{2}+2x-15=0)
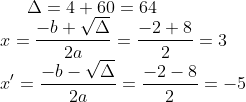
C(3,7)
C(-5,1)
Portanto a equação da reta BC vale.

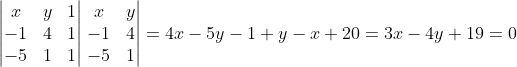
Fazemos o mesmo procedimento para encontrar o vértice D.
A reta AD tem coeficiente angular igual a 3/4.
O ponto a pertence a reta AD.
\rightarrow y=\frac{3}{4}(x-2)\rightarrow y=\frac{3x}{4}-\frac{6}{4}\rightarrow y=\frac{3x}{4}-\frac{3}{2})
As coordenadas do ponto D:
D(x,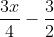 )
)
^{2}+\left ( \frac{3x}{4}-\frac{3}{2} \right )^{2}\rightarrow 25=x^{2}-4x+4+\frac{9x^{2}}{16}-\frac{18x}{8}+\frac{9}{4}\rightarrow 25=\frac{25x^{2}}{16}-\frac{50x}{8}+\frac{25}{4}=25\rightarrow 25x^{2}-100x-300=0\rightarrow x^{2}-4x-12=0)
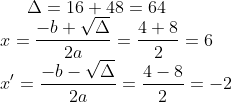
D(6,3)
D(-2,-3)
Portanto a equação da reta AD vale.
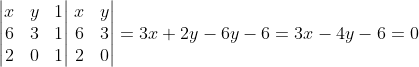
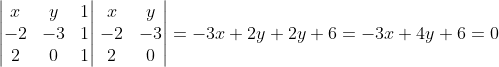
Reta CD.
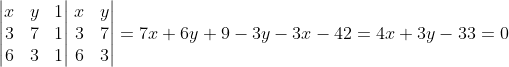
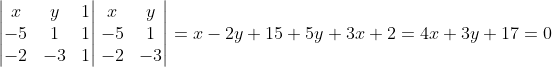
Reta AB
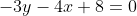
Espero ter ajudado.
Sendo esta a equação da reta AB, e tendo coeficiente angular igual a:m=-4/3.
A reta BC é perpendicular a reta AB,portanto ela tem coeficiente angular igual a:
O ponto B(-1,4), pertence a reta BC portanto.
O ponto C vai ter como coordenadas.
(x,
Encontramos agora a medida do lado do quadrado.
Encontramos assim o valor de x.
C(3,7)
C(-5,1)
Portanto a equação da reta BC vale.
Fazemos o mesmo procedimento para encontrar o vértice D.
A reta AD tem coeficiente angular igual a 3/4.
O ponto a pertence a reta AD.
As coordenadas do ponto D:
D(x,
D(6,3)
D(-2,-3)
Portanto a equação da reta AD vale.
Reta CD.
Reta AB
Espero ter ajudado.

William Carlos- Jedi

- Mensagens : 432
Data de inscrição : 06/07/2012
Idade : 30
Localização : São Carlos-SP
 Re: vértices do quadrado
Re: vértices do quadrado
Obg limonada pela ajuda e tbm william, mas william eu nao entendi pq para encontrar o valor de x vc fez:
25=(x+1)²+((3x/4+19/4)-4)²
nao entendi se vc usou alguma formula, e o por que o x+1
25=(x+1)²+((3x/4+19/4)-4)²
nao entendi se vc usou alguma formula, e o por que o x+1

jessicajessica- Jedi

- Mensagens : 418
Data de inscrição : 18/05/2012
Idade : 29
Localização : Arujá, SP

William Carlos- Jedi

- Mensagens : 432
Data de inscrição : 06/07/2012
Idade : 30
Localização : São Carlos-SP
 Re: vértices do quadrado
Re: vértices do quadrado
obg, estava meio distraida, mas entendi agora 

jessicajessica- Jedi

- Mensagens : 418
Data de inscrição : 18/05/2012
Idade : 29
Localização : Arujá, SP
 Re: vértices do quadrado
Re: vértices do quadrado
Sem problemas.

William Carlos- Jedi

- Mensagens : 432
Data de inscrição : 06/07/2012
Idade : 30
Localização : São Carlos-SP
 Tópicos semelhantes
Tópicos semelhantes» Quadrado e vértices
» Vertices de um quadrado
» vértices de um quadrado
» Vértices de um quadrado
» Vértices de um quadrado.
» Vertices de um quadrado
» vértices de um quadrado
» Vértices de um quadrado
» Vértices de um quadrado.
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












