Um canal de navegação de 4,0m

por Vieira1 Sex 03 Ago 2012, 17:31

(FUVEST-SP) Um canal de navegação de 4,0m de largura tem suas comportas semi-abertas, como está indicado na figura. Ondas planas propagam-se na superfície da água do canal com velocidade igual a 2,0m/s. Considere uma crista AB, na posição indicada na figura, no instante t=0.

Esboce a configuração dessa crista depois de decorridos 1,5s, indicando a distância, em metros, entre seus extremos A’B’ nessa configuração (despreze efeitos da difração)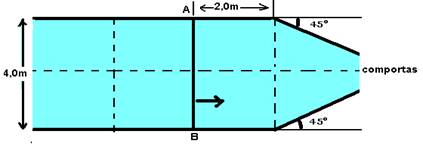 Um canal de navegação de 4,0m Image054

por **Eduardo Sicale** Sáb 04 Ago 2012, 19:57

por **Al.Henrique** Sáb 04 Ago 2012, 20:21

Boa noite Edu,

você poderia, por gentileza, demonstrar os cálculos para concluir que d = 2m?

por **Eduardo Sicale** Sáb 04 Ago 2012, 21:26

v = Delta s / Delta t ---> 2 = Delta s/1,5 ---> Delta s = 3,0 m

Note que 3 metros é a distância percorrida pelas ondas. Como para atingir as comportas temos 2 metros, as ondas avançam 1 metro esbarrando nas comportas. Sabemos o ângulo das comportas, que é de 45°, então, pelo teorema de Pitágoras, descobrimos que as ondas refletidas avançam 1 metro de cada lado em direção à linha central do canal. As ondas que não sofreram reflexão são a diferença entre 4 m, que é a largura do canal, e 1 m de cada lado, resultando 2 m.