EPCAr 2006- Geometria
2 participantes
Página 1 de 1
EPCAr 2006- Geometria
por YuriMarinho(: Sex 27 Jul 2012, 09:04
Um piloto de avião, a uma altura de 3100 m em relação ao
solo, avista o ponto mais alto de um edifício de 100 m de
altura nos instantes T1 e T2, sob os ângulos de 45° e 30°,
respectivamente, conforme a figura seguinte:
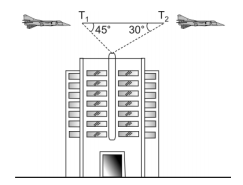
A distância percorrida pelo avião entre T1 e T2, é, em m,
igual a:
a) 3000(1+ √3 ) c) 2190 √3
b) 3000 √3 d) 3000(√3 −1)
solo, avista o ponto mais alto de um edifício de 100 m de
altura nos instantes T1 e T2, sob os ângulos de 45° e 30°,
respectivamente, conforme a figura seguinte:
A distância percorrida pelo avião entre T1 e T2, é, em m,
igual a:
a) 3000(1+ √3 ) c) 2190 √3
b) 3000 √3 d) 3000(√3 −1)
YuriMarinho(:- Padawan
- Mensagens : 89
Data de inscrição : 17/07/2012
Idade : 26
Localização : Rio de Janeiro . Rj Brasil
Re: EPCAr 2006- Geometria
por JoaoGabriel Sex 27 Jul 2012, 12:35
A distância entre a vertical do prédio e a horizontal do avião é 3100 - 100 = 3000m.
Denotemos por d a distância pedida.
Do ponto mais alto do prédio, de onde partem as duas linhas tracejadas, trace uma linha vertical , perpendicular ao deslocamento d. Note que esta linha dividirá d em 2 trechos, que chamaremos x e y. Sabemos o comprimento desta linha, é o 3000 m anteriormente calculado. Aplicando a tangente, temos:
3000/x = tg 45 --> x = 3000
3000/y = V3/3 --> y*V3 = 3000* V3*V3 --> y = 3000*V3
Temos que d = x + y, logo:
d = 3000 + 3000*V3 = 3000(1 + V3) A
Acho que é isso, abraços
Denotemos por d a distância pedida.
Do ponto mais alto do prédio, de onde partem as duas linhas tracejadas, trace uma linha vertical , perpendicular ao deslocamento d. Note que esta linha dividirá d em 2 trechos, que chamaremos x e y. Sabemos o comprimento desta linha, é o 3000 m anteriormente calculado. Aplicando a tangente, temos:
3000/x = tg 45 --> x = 3000
3000/y = V3/3 --> y*V3 = 3000* V3*V3 --> y = 3000*V3
Temos que d = x + y, logo:
d = 3000 + 3000*V3 = 3000(1 + V3) A
Acho que é isso, abraços
JoaoGabriel- Monitor
- Mensagens : 2344
Data de inscrição : 30/09/2010
Idade : 29
Localização : Rio de Janeiro
Tópicos semelhantes» EPCAR 2006 Geometria
» EPCAR 2006 Geometria - 24
» EPCAr 2006- Geometria
» EPCAR 2006/2007 geometria
» (EPCAr-2006) Geometria Plana : Questão 21
» EPCAR 2006 Geometria - 24
» EPCAr 2006- Geometria
» EPCAR 2006/2007 geometria
» (EPCAr-2006) Geometria Plana : Questão 21
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
