Divisão de polinômios
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Divisão de polinômios
Divisão de polinômios
Encontre o resto da divisão de 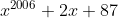 por
por 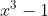
phBorges_32- Iniciante
- Mensagens : 39
Data de inscrição : 24/02/2024
Idade : 20
Localização : Rio de janeiro
 Re: Divisão de polinômios
Re: Divisão de polinômios
Usando que \(t^n - 1)\) é divisível por \((t - 1\), segue que \( x^{2004} - 1 = (x^3)^{668} - 1\) é divisível por \( x^3 -1\). Ou seja, existe um polinomio q(x) tal que
\( x^{2004} - 1= q(x) (x^3 -1) \implies \)
\(x^{2006} - x^2 = x^2 q(x) (x^3-1) \implies \)
\( x^{2006} + 2x+87 = x^2 q(x) (x^3-1) + x^2 +2x+87\)
Portanto, o resto é x² +2x+87
Obs.: Outra maneira de pensar é observar que sendo r uma raiz de x³ -1, então r³ = . Daí, se \(p(x) = x^{2006} + 2x+87\), temos p(r) = r² + 2r+87. Esse deve ser o resto.
\( x^{2004} - 1= q(x) (x^3 -1) \implies \)
\(x^{2006} - x^2 = x^2 q(x) (x^3-1) \implies \)
\( x^{2006} + 2x+87 = x^2 q(x) (x^3-1) + x^2 +2x+87\)
Portanto, o resto é x² +2x+87
Obs.: Outra maneira de pensar é observar que sendo r uma raiz de x³ -1, então r³ = . Daí, se \(p(x) = x^{2006} + 2x+87\), temos p(r) = r² + 2r+87. Esse deve ser o resto.

DaoSeek- Jedi

- Mensagens : 316
Data de inscrição : 29/07/2022
 Tópicos semelhantes
Tópicos semelhantes» divisão de polinômios!
» Divisão de polinomios.
» Divisão de polinômios
» Divisão de Polinômios
» Divisão de polinômios
» Divisão de polinomios.
» Divisão de polinômios
» Divisão de Polinômios
» Divisão de polinômios
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












