Álgebra Vetorial - Circunferência R³
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Álgebra Vetorial - Circunferência R³
por Júliawww_520 29/7/2024, 3:09 pm
O raio da circunferência
Resposta: 4.
Resposta: 4.
Júliawww_520- Jedi
- Mensagens : 423
Data de inscrição : 08/02/2022
Idade : 21
Localização : Rio de Janeiro, RJ
Re: Álgebra Vetorial - Circunferência R³
por Lipo_f 29/7/2024, 4:11 pm
x² + y² + z² + 2x + 4y + 6z = 11
(x² + 2x + 1) + (y² + 4y + 4) + (z² + 6z + 9) = 11 + 1 + 4 + 9
(x+1)² + (y+2)² + (z+3)² = 5²
Estamos seccionando uma esfera de raio 5 com um plano que é dado. A fórmula para calcular a distância do centro da circunferência (-1,-2,-3) ao plano é análoga da analítica no R2:
d = |2.-1 + 3.-2 + 6.-3 + 5|/√2² + 3² + 6² = 21/7 = 3.
Tomo a liberdade de usar esta imagem para ilustrar:
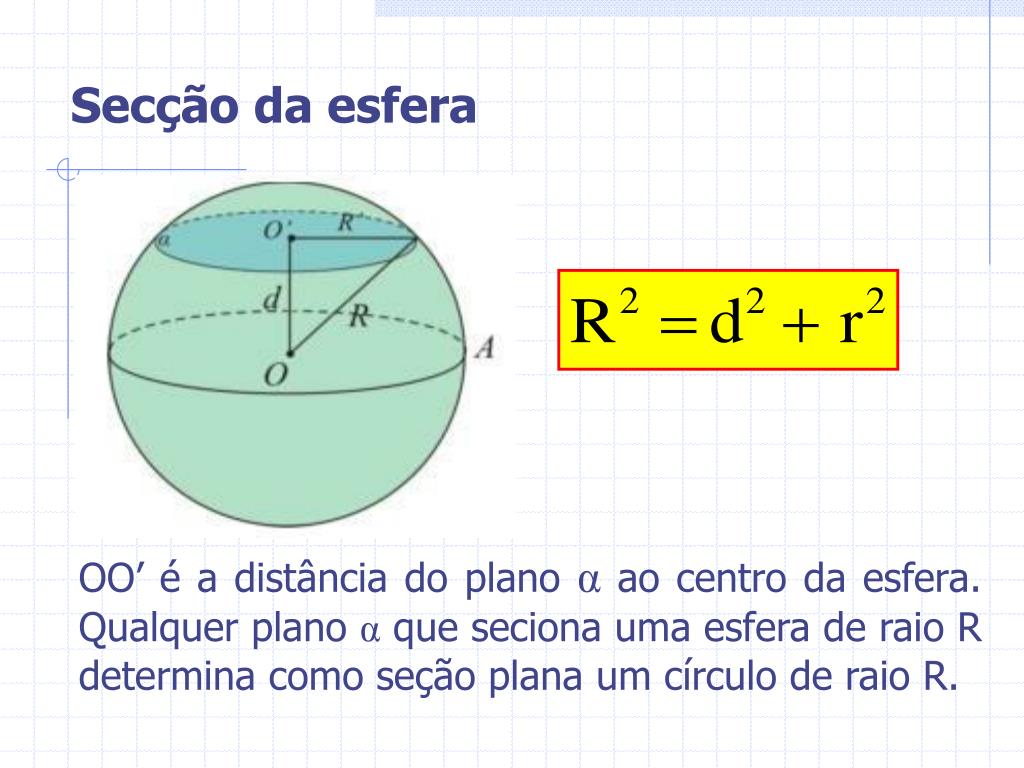
Seguindo então que R² = d² + r² => 5² = 3² + r² => r = 4.
(x² + 2x + 1) + (y² + 4y + 4) + (z² + 6z + 9) = 11 + 1 + 4 + 9
(x+1)² + (y+2)² + (z+3)² = 5²
Estamos seccionando uma esfera de raio 5 com um plano que é dado. A fórmula para calcular a distância do centro da circunferência (-1,-2,-3) ao plano é análoga da analítica no R2:
d = |2.-1 + 3.-2 + 6.-3 + 5|/√2² + 3² + 6² = 21/7 = 3.
Tomo a liberdade de usar esta imagem para ilustrar:
Seguindo então que R² = d² + r² => 5² = 3² + r² => r = 4.
Lipo_f- Mestre Jedi
- Mensagens : 535
Data de inscrição : 16/05/2024
Idade : 19
Localização : Belém, Pará
Tópicos semelhantesPiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
