Geometria Analítica, envolvendo planos e parábolas.

por TheMugha Sex 22 Dez 2023, 19:39

Boa Noite meus caros, estou precisando da resolução para esta questão aqui de uma prova em inglês, já procurei em outros lugares, porém não consigo encontrar...

2. On the xy-plane, a circle with center (a, b) and radius r is tangent to the parabola y = r² at two distinct points.
Fill in the blanks with the answers to the following questions.
(1) When one of the two points of tangency is (t, t2), express a, b, and r in terms of t.
a=
b=
T=
(2) When one of the two points of tangency is (1/2, 1/4) express the area S of the finite region bounded by the circle and the parabola in terms of .
S =

as respostas são as seguintes:
a = 0
b = t² + 0.5
r = √(t² + 0.25)
S = (5/12)-(1/8pi)

Caso consigam resolver será de grande ajuda para meus estudos.. Obrigado!

por **Giovana Martins** Sex 22 Dez 2023, 22:06

Primeiramente, peço que confira os cálculos, pois eu os fiz, mas não revisei. Chegou no seu gabarito, mas se houver qualquer erro, me avise. Ademais, eu fui bem direta nos cálculos, especialmente no cálculo da integral, pois eu parti do princípio de que você já está habituado a calcular integrais. De qualquer modo, se houver dúvidas, me avise que eu explicito mais os cálculos.

Do enunciado: (x - a)² + (y - b)² = r² e y = x², que são tangentes no ponto (t,t²) e (x,y).

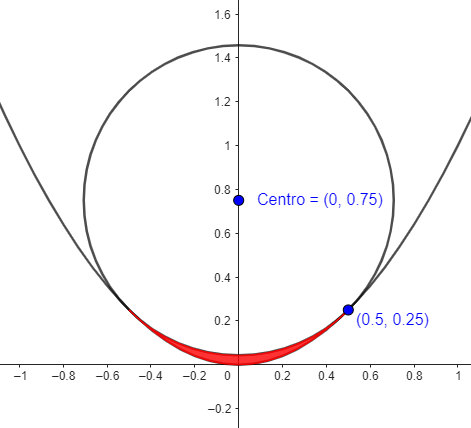
Dada a configuração da parábola e sendo (a,b) o centro da circunferência, sem fazer contas podemos afirmar que a = 0. Irei mostrar isso abaixo com uma figura ilustrativa.

Geometria Analítica, envolvendo planos e parábolas. Oie_t166

Deste modo, podemos escrever a equação da circunferência da seguinte forma: x² + (y - b)² = r².

No ponto de tangência x² + (y - b)² = r² e y = x² tem a mesma inclinação. Derivando implicitamente x² + (y - b)² = r² e y = x², além do fato de que (t,t²) é um dos pontos de tangência:

[latex]\\\mathrm{\frac{d}{dx}\left [ x^2 + (y - b)^2 \right ]=\frac{d}{dx}(r^2)\ \therefore\ \frac{dy}{dx}=-\frac{x}{y-b}=\frac{d}{dx}\left ( x^2 \right )}\\\\ \mathrm{\ \ Manipulando\ a\ igualdade:-\frac{x}{y-b}=2x.\ Para\ (t,t^2):}\\\\ \mathrm{Chega-se\ em\ \frac{t}{t^2-b}=-2t.\ Como\ t\neq 0:\boxed {\mathrm{b=t^2+0.5}}}[/latex]

Da igualdade x² + (y - b)² = r² e do ponto de tangência, além da última expressão de b que encontramos:

[latex]\\\mathrm{t^2 + \left ( t^2-t^2-0.5 \right )^2 =r^2\ \therefore\ \boxed {\mathrm{r=\sqrt{t^2+0.25}}}}[/latex]

Para o item B), sendo (t,t²) = (0.5,0.25), logo, a = 0, b = 0.75 e r² = 0.5. Deste modo: x² + (y - 0.75)² = 0.5. Para o cálculo da área tem-se:

[latex]\\\mathrm{x^2+\left ( y-\frac{3}{4} \right )^2=\frac{1}{2}\to y=\frac{3}{4}\pm\sqrt{\frac{1}{2}-x^2}}[/latex]

[latex]\mathrm{S=\int_{-\frac{1}{2}}^{\frac{1}{2}}\left [ \left ( \frac{3}{4}-\sqrt{\frac{1}{2}-x^2} \right )-x^2 \right ]dx=-\frac{1}{\sqrt{2}}\int \sqrt{1-2x^2}dx-\int x^2dx+\int \frac{3}{4}dx}[/latex]

[latex]\mathrm{x=\frac{1}{\sqrt{2}}sin(\phi )\to \phi =arcsin\left (x\sqrt{2} \right )\to dx=\frac{1}{\sqrt{2}}cos(\phi )d\phi }[/latex]

[latex]\mathrm{\int \sqrt{1-2x^2}dx=\int \frac{cos(\phi )\sqrt{1-sin^2(\phi )}}{\sqrt{2}}d\phi =\frac{1}{\sqrt{2}}\int cos^2(\phi )d\phi =\frac{1}{2}sin(\phi )cos(\phi )+\int \frac{1}{2}d\phi }[/latex]

[latex]\mathrm{\therefore\ \int \sqrt{1-2x^2}dx=\frac{1}{2\sqrt{2}}arcsin\left ( x\sqrt{2} \right )+\frac{1}{2}x\sqrt{1-2x^2}}[/latex]

[latex]\mathrm{S=\int_{-\frac{1}{2}}^{\frac{1}{2}}\left [ \left ( \frac{3}{4}-\sqrt{\frac{1}{2}-x^2} \right )-x^2 \right ]dx=\left [-\frac{1}{4}arcsin\left ( x\sqrt{2} \right )-\frac{1}{2\sqrt{2}}x\sqrt{1-2x^2}-\frac{1}{3}x^3+\frac{3}{4}x \right ]_{-\frac{1}{2}}^{\frac{1}{2}}}[/latex]

[latex]\mathrm{\boxed {\mathrm{S=\int_{-\frac{1}{2}}^{\frac{1}{2}}\left [ \left ( \frac{3}{4}-\sqrt{\frac{1}{2}-x^2} \right )-x^2 \right ]dx=\frac{5}{12}-\frac{\pi }{8}}}}[/latex]

por **Giovana Martins** Sex 22 Dez 2023, 22:23

Para facilitar a sua vida, no cálculo da integral na qual eu utilizei substituições trigonométricas, utilize a identidade 2cos²(x) = 1 + cos(2x) que a conta fica mais fácil.