Equações de reta no plano

Determine as equaçoes das retas que passam pelo ponto (2, −1) e formam, cada uma, um angulo
de [latex] \frac{\pi}{3}[/latex] radianos com a reta 2x − 3y + 7 = 0.

Considere a reta dada como r, e as faltantes como retas s e t.
[latex] r:2x-3y+7=0\rightarrow m_r=\frac{2}{3} [/latex]
Queremos que as retas s e t formem 60 graus com a reta r, portanto, utilizando a equação do ângulo entre retas:
[latex] tg\theta =\left | \frac{m_r-m'}{1+m_r.m'} \right | \rightarrow \pm \sqrt{3}=\frac{2-3m'}{3+2m'} [/latex]
Resolvendo a equação você obtêm os seguintes valores:
[latex] m'=-8+13\frac{\sqrt{3}}{3} \: \: ou \: \: m'=-8-13\frac{\sqrt{3}}{3} [/latex]
Sabendo os valores dos coeficientes angulares e que as retas passam pelo ponto (2, -1), basta encontrar as equações:
[latex] y-y_p=m(x-x_p) 
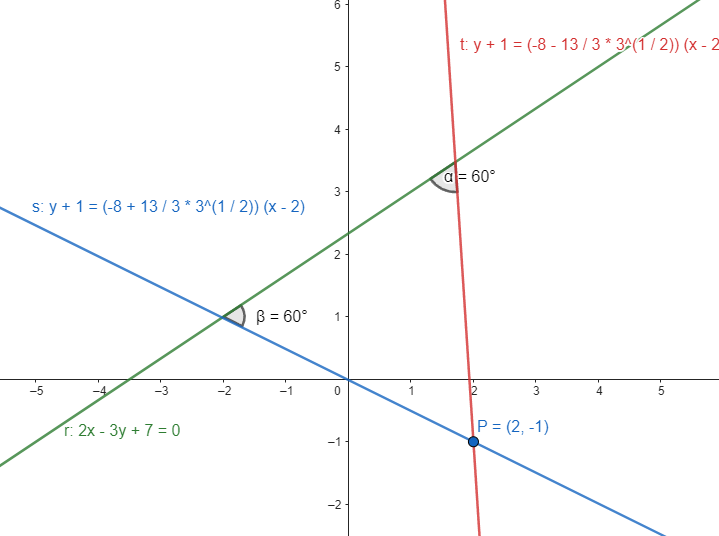
s:y+1=(-8+\frac{13\sqrt{3}}{3})(x-2) 
t: y+1=(-8-\frac{13\sqrt{3}}{3})(x-2) [/latex]