MATRIZES BINÁRIAS-TEORIA DAS PROBABILIDADES

Meu primeiro post neste Forum!

Por estar a aprender Python (linguagem de programação informática), criei um programa, cuja função é gerar aleatoriamente 16 milhões de pares de matrizes 2x2 binárias, verificar se são iguais, e quando são, registar em Base de Dados o numeral indicativo das vezes necessárias para que a combinação certeira acontecesse. Da própria natureza do cálculo de probabilidades do problema em causa, resulta que 2 à potência de 4 = 16, significa que a probabilidade de que dois pares gerados consecutivamente sejam iguais é de 1 para 16. Posto isto, e por que a teoria é, no infinito da amostragem, infinitamente exata, o programa gerou aproximadamente o tal milhão de extrações ganhadoras.

Após isto, o programa analisou na Base de Dados entretando formada com aprox. 1 milhão de registos, quantas vezes a mesma ocorrência de frequência certeira foi encontrada. Sendo o registo de frequência mais elevado de valor 191, obtive de resposta uma coleção de 180 elementos, pois que a range para o final dos 191 não era absolutamente consecutiva (creio que por escassez da amostra de 1 milhão de acertos). A figura seguinte, ilustra a distribuição da quantidade de vezes MATCH por cada um dos 180 elementos apurados.


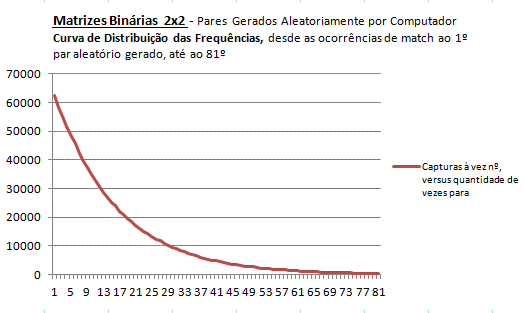
Note-se que desprezei os elementos a partir do 81 ao 191, porque sendo as suas frequências tão baixas, apenas alongaria a curva, não contribuindo para uma melhor evidência visual.

1) Como é que o acaso resolveu que onde acontece mais vezes o MATCH é ao primeiro par de matrizes gerado, distribuindo por regressão em curva da quantidade de vezes para o acerto, pelos elementos seguintes em análise, i.e. o um, o dois, o três,  o quatro, o n..., tendendo para + infinito?

2) Por que razão, a ordem dos elementos em análise é tão religiosamente sequencial? Como é que o acaso decidiu que o elemento 4 (à quarta vez) acontece mais um pouquinho de vezes que o elemento 5 (à quinta vez)? E o mesmo em relação ao elemento 5 e 6, e ao 6 e ao 7, até desaparecer no infinito?

Presumindo que não existe um vício de raciocínio meu, muito espantado fiquei com os resultados da experiência, que no início se destinava a melhorar a minha prática em programação, o que acabou por acontecer de qualquer modo, mas que não evitou após isso, a ideia de aproveitar o esforço da exploração da função RANDOMIZE, em prol de desafiar o pouco que já sabia da teoria das probabilidades, pois que não estava disponível para atirar ao ar uma moeda 256 milhões de vezes (16 milhões x 8 + 16 milhões x , quantidade suficiente para gerar 2 pares de 16 milhões de matrizes binárias, suficientes para os tais aproximadamente 1 milhão de acertos "MATCH", meta inicialmente proposta.

Agradeço muito a vossa colaboração para me ajudar a compreender a natureza deste fenómeno, no meu modesto entender, bizarro. Para mim, a distribuição devia ser equitativa, pelo menos durante os primeiros 16 elementos da coleção (do 1 ao 16) e não, imediatamente decrescente (em parábola) logo a partir do primeiro elemento, como demonstrou a minha experiência. Obrigado a todos!

O problema deve ter a ver com o algoritmo pseudoaleatório que o computador usa para gerar as matrizes binárias.

Obrigado pela resposta, também suspeitei que fosse algo assim. Roubo-lhe mais um pouco de tempo: o algoritmo vai gerar tantos pares de matrizes quantos os escolhidos pelo user. De seguida gera a primeira matriz 2x2 e só depois gera a segunda.

As matrizes são geradas correndo uma função random, que gera um de dois resultados 0 ou 1, e deposita-o na 1º linha e 1ª coluna da matriz. De seguida faz o mesmo para linha 1 coluna 2, linha 2 coluna 1 e linha 2 coluna 2, completando assim as 4 quadrículas da matriz.

Imediatamente a seguir à criação do primeiro par de matrizes, o algoritmo compara-as e se não forem iguais gera outro par. Vai gerar pares de matrizes sucessivamente até à comparação encontrar igualdade. Neste momento guarda na Base de dados o registo do numeral do numero de vezes que gerou pares até aqui. A seguir continua a gerar pares de matrizes até nova igualdade com registo idêntico na Base de Dados. Em algum momento atinge o limite de extrações imposto pelo user no início e pára a execução.

Esta é a descrição pormenorizada da sequência de ações do algoritmo.
Não consigo perceber onde está a deficiência, poderá ajudar-me? Muito obrigado.