Pirâmide

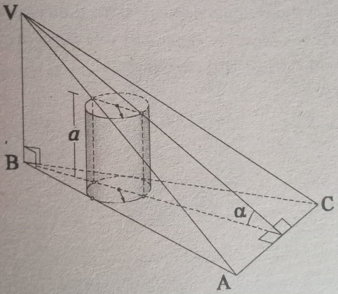
A pirâmide V-ABC tem sua base ABC regular, VB é perpendicular ao plano do triângulo ABC, a base inferior do cilindro toca em AB e BC e a superior toca nas faces laterais da pirâmide. Se: AB=2a, calcule o valor mínimo de [latex]\alpha [/latex].


a)[latex]29^{\circ}[/latex]
b)[latex]30^{\circ}[/latex]
c)[latex]31^{\circ}[/latex]
d)[latex]44^{\circ}[/latex]
e)[latex]46^{\circ}[/latex]


R:c

Suponha que vamos encolhendo o raio do cilindro até que fique zero: r = 0. Neste caso, como a borda do cilindro toca a face superior da pirâmide, a altura que marquei como a (fig. direita) vai se deslocando para a esquerda até que tenhamos a = y. Nesta situação a tangente do ângulo é:

Porém o cilindro existe e consequentemente seu raio por menor que seja não pode ser zero, deve ser maior: r > 0. Isto força aquela borda do cilindro onde marcamos a altura a para a direita, o que força o ângulo da base com a face superior ser maior do que 30º. Portanto devemos ter  [latex]\,\,\alpha > 30^{\circ}[/latex]. Se nos atermos a valores inteiros do ângulo, conclui-se que