Quadriláteros

por jjbr4603 Sáb 05 Mar 2022, 10:27

Dentre todos os paralelogramos ABCD com AB=AC=7, o de área máxima tem área igual a

A) 49 B) 49[latex]\sqrt{2}[/latex] C) [latex]\frac{49\sqrt{3}}{2}[/latex] D)[latex]\frac{49}{2}[/latex] E) NDA

Gabarito letra A

Alguém sabe como faz essa?

por **tales amaral** Sáb 05 Mar 2022, 10:57

Quadriláteros QBiFGVgW8QsCNiW+gG0XXSBzewY2Jb6AcQqqsDmNB4AQI6iCmwA2zLhA2IWTWBTbAGAXEUT2BYR1oB1mPABsYs6sAEA5CCawOaM00CZ1BAgJlFd6UCBBTblVB5ACqLpsAGUxeQPiI3ABiRLdw1IhcAGZEV3DYiRwAYkSXcNSInABmRDdw2IlcAGJEd3DUiNwAZkQXcNiJnABiRFdw1IkcAGJE93DYidwAYkQ3cNSJXABiRNdw1IgcAGJEF3DUiZwAYkS3cNSIXABkRPdw1IncAGANByAhsQtWXdNZtDgZQIbAAALSewAdHSXQNyIbABALScwAYkRXcNSJHABkTJqTyAnAhsQDJ014BUCWxAdHTXgNwIbEASdNeAlAlsQFR014AcCWxA9HTXgNQJbEA0dNeAXAlsQNR014AcCGxAFHTXgJwJbEC0dNeAXAhsQOvprgG5E9iAKOmuATkR2IBW010DENiACOmuAbkR2IDW0l0DeE9gA6KiuwbkSGADWkl3DeBHAhsAQMsJbEDrLOuu2RwK5EpgAwBoOYENaBXdNYDbBDYAgJYT2IDW010DciewAa3hVB4AiwlsQKvprgEIbEBL6K4BLCewAa2luwbwnsAGNE53DeBuAhvQSrprAD8S2IBG6a4BrCawAa2juwYwS2ADGqO7BrAegQ1oFd01gNsENgCAlhPYgMbMd9N01wAW+7DpAQB5E9IAVvsfnTIchRHmY58AAAAASUVORK5CYII=

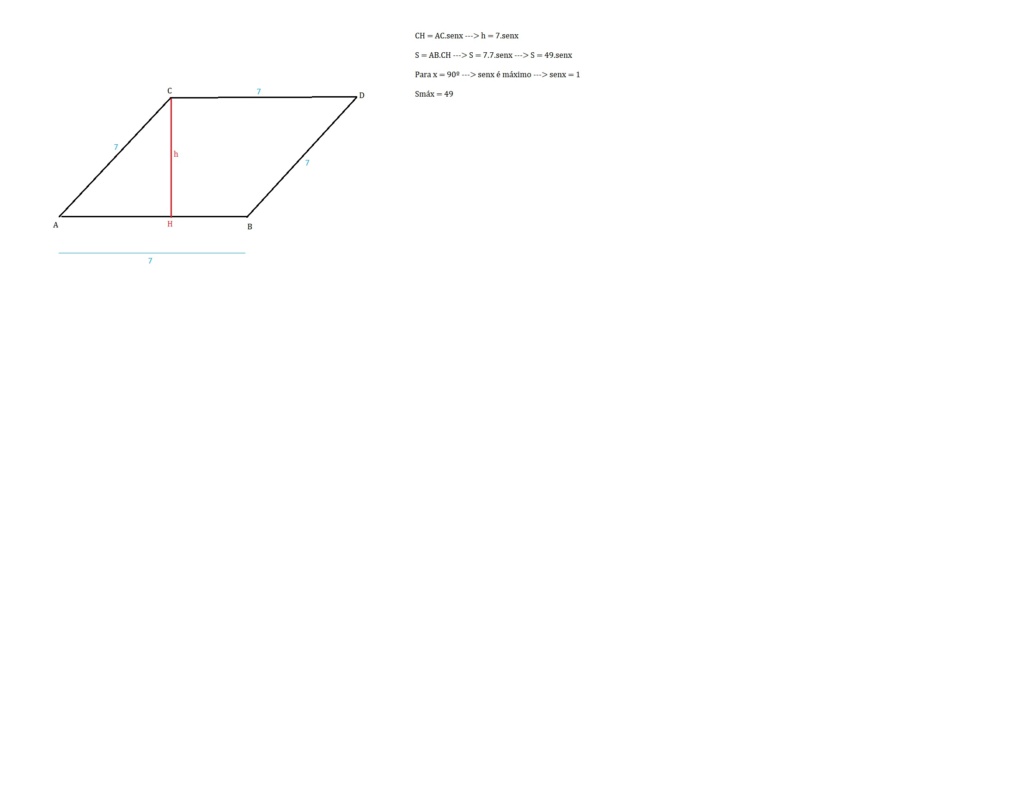
A área é [latex]A = 2 \cdot \left(\dfrac{7\cdot 7 \cdot \text{sen} (x)}{2} \right )[/latex]. Seu valor máximo ocorre quando sen(x) = 1 e é dado por [latex]A = 2 \cdot \left(\dfrac{7\cdot 7 \cdot 1}{2} \right ) = 49[/latex].

por **Giovana Martins** Sáb 05 Mar 2022, 10:58

[latex]\\\mathrm{Seja\ o\ quadril\acute{a}tero\ de\ lados\ x\ e\ y\ e\ p\ o\ perimetro\ do\ quadril\acute{a}tero.}\\\\\mathrm{Logo, x+y=\frac{p}{2}.\ Sendo\ A(x,y)=xy=x\left ( \frac{p}{2}-x \right )=-x^2+\frac{px}{2}=A(x).}\\\\\mathrm{A(x)\to polin\hat{o}mio\ do\ 2^{\circ}\ grau,logo:M\acute{a}x(x_V,y_V=A_{m\acute{a}x}).}\\\\\mathrm{Portanto:x_V=-\frac{b}{2a}=\frac{p}{4}\ \therefore \ De\ x+y=\frac{p}{2}\to y=\frac{p}{2}-\frac{p}{4}=\frac{p}{4}}\\\\\mathrm{Note\ que\ A(x)=A_{m\acute{a}x}\ se\ x=y=\frac{p}{4},isto\ \acute{e},se\ o\ quadril\acute{a}tero\ \acute{e}\ um\ quadrado.}\\\\\mathrm{Agora\ que\ sabemos\ que\ de\ todos\ os\ quadril\acute{a}teros, o\ de\ maior\ \acute{a}rea\ \acute{e}\ o\ quadrado,}\\\\\mathrm{para\ \overline{AB}=\overline{AC}=7,tem-se:A_{m\acute{a}x}=7\times 7=49.}[/latex]

por **Giovana Martins** Sáb 05 Mar 2022, 11:50

tales amaral escreveu:

A área é [latex]A = 2 \cdot \left(\dfrac{7\cdot 7 \cdot \text{sen} (x)}{2} \right )[/latex]. Seu valor máximo ocorre quando sen(x) = 1 e é dado por [latex]A = 2 \cdot \left(\dfrac{7\cdot 7 \cdot 1}{2} \right ) = 49[/latex].

Tales, estou meio enferrujada em geometria plana. O que garante que a diagonal do quadrilátero vale 7? A propósito, ainda que esteja correto o valor da diagonal, respeitosamente, a sua resolução me parece um tanto equivocada. Como garantimos que o quadrilátero de maior área é de fato um losango? Na minha resolução eu parti de um quadrilátero genérico até concluir que o quadrilátero de área máxima é um quadrado ao invés de um losango.

Digamos que eu tivesse partido da suposição de que o losango, ao invés de um retângulo como eu fiz inicialmente, fosse o quadrilátero de maior área:

[latex]\\\mathrm{Seja\ o\ quadril\acute{a}tero\ de\ diagonais\ x\ e\ y\ e\ p\ o\ perimetro\ do\ quadril\acute{a}tero.}\\\\\mathrm{Logo, \frac{p}{4}=\frac{1}{2}\sqrt{x^2+y^2}\ \therefore \ y=\sqrt{\frac{p^2}{4}-x^2}\ \therefore \ A(x,y)=\frac{xy}{2}=\frac{x}{2}\sqrt{\frac{p^2}{4}-x^2}=A(x)}\\\\\mathrm{\frac{dA(x)}{dx}=\frac{d}{d}\left ( \frac{x}{2}\sqrt{\frac{p^2}{4}-x^2} \right )=\frac{p^2-8x^2}{4\sqrt{-4x^2+p^2}}=0\to x=\frac{p\sqrt{2}}{4}\ \therefore \ y=\frac{p\sqrt{2}}{4}}\\\\\mathrm{Sendo\ x=y=\frac{p\sqrt{2}}{4}\ \therefore \ O\ quadril\acute{a}tero\ de\ maior\ \acute{a}rea\ \acute{e}\ um\ quadrado.}[/latex]

Nota: eu apelei para as derivadas pelo pouco tempo que tenho agora, mas dá para encontrar os maximizadores de A(x) sem derivadas. Logo mais eu posto.

por jjbr4603 Sáb 05 Mar 2022, 12:10

obrigado Giovana e Tales. Smile

por **tales amaral** Sáb 05 Mar 2022, 15:35

Giovana Martins escreveu:
tales amaral escreveu:

A área é [latex]A = 2 \cdot \left(\dfrac{7\cdot 7 \cdot \text{sen} (x)}{2} \right )[/latex]. Seu valor máximo ocorre quando sen(x) = 1 e é dado por [latex]A = 2 \cdot \left(\dfrac{7\cdot 7 \cdot 1}{2} \right ) = 49[/latex].

Tales, estou meio enferrujada em geometria plana. O que garante que a diagonal do quadrilátero vale 7? A propósito, ainda que esteja correto o valor da diagonal, respeitosamente, a sua resolução me parece um tanto equivocada. Como garantimos que o quadrilátero de maior área é de fato um losango? Na minha resolução eu parti de um quadrilátero genérico até concluir que o quadrilátero de área máxima é um quadrado ao invés de um losango.

Digamos que eu tivesse partido da suposição de que o losango, ao invés de um retângulo como eu fiz inicialmente, fosse o quadrilátero de maior área:

[latex]\\\mathrm{Seja\ o\ quadril\acute{a}tero\ de\ diagonais\ x\ e\ y\ e\ p\ o\ perimetro\ do\ quadril\acute{a}tero.}\\\\\mathrm{Logo, \frac{p}{4}=\frac{1}{2}\sqrt{x^2+y^2}\ \therefore \ y=\sqrt{\frac{p^2}{4}-x^2}\ \therefore \ A(x,y)=\frac{xy}{2}=\frac{x}{2}\sqrt{\frac{p^2}{4}-x^2}=A(x)}\\\\\mathrm{\frac{dA(x)}{dx}=\frac{d}{d}\left ( \frac{x}{2}\sqrt{\frac{p^2}{4}-x^2} \right )=\frac{p^2-8x^2}{4\sqrt{-4x^2+p^2}}=0\to x=\frac{p\sqrt{2}}{4}\ \therefore \ y=\frac{p\sqrt{2}}{4}}\\\\\mathrm{Sendo\ x=y=\frac{p\sqrt{2}}{4}\ \therefore \ O\ quadril\acute{a}tero\ de\ maior\ \acute{a}rea\ \acute{e}\ um\ quadrado.}[/latex]

Nota: eu apelei para as derivadas pelo pouco tempo que tenho agora, mas dá para encontrar os maximizadores de A(x) sem derivadas. Logo mais eu posto.

A diagonal é o segmento AC, portanto é igual a 7. O resto parte da análise do seno de um ângulo (valor máximo 1). Os dois ângulos ali são iguais pois é um paralelogramo.

por **Giovana Martins** Sáb 05 Mar 2022, 15:50

tales amaral escreveu:
Giovana Martins escreveu:
tales amaral escreveu:

A área é [latex]A = 2 \cdot \left(\dfrac{7\cdot 7 \cdot \text{sen} (x)}{2} \right )[/latex]. Seu valor máximo ocorre quando sen(x) = 1 e é dado por [latex]A = 2 \cdot \left(\dfrac{7\cdot 7 \cdot 1}{2} \right ) = 49[/latex].

Tales, estou meio enferrujada em geometria plana. O que garante que a diagonal do quadrilátero vale 7? A propósito, ainda que esteja correto o valor da diagonal, respeitosamente, a sua resolução me parece um tanto equivocada. Como garantimos que o quadrilátero de maior área é de fato um losango? Na minha resolução eu parti de um quadrilátero genérico até concluir que o quadrilátero de área máxima é um quadrado ao invés de um losango.

Digamos que eu tivesse partido da suposição de que o losango, ao invés de um retângulo como eu fiz inicialmente, fosse o quadrilátero de maior área:

[latex]\\\mathrm{Seja\ o\ quadril\acute{a}tero\ de\ diagonais\ x\ e\ y\ e\ p\ o\ perimetro\ do\ quadril\acute{a}tero.}\\\\\mathrm{Logo, \frac{p}{4}=\frac{1}{2}\sqrt{x^2+y^2}\ \therefore \ y=\sqrt{\frac{p^2}{4}-x^2}\ \therefore \ A(x,y)=\frac{xy}{2}=\frac{x}{2}\sqrt{\frac{p^2}{4}-x^2}=A(x)}\\\\\mathrm{\frac{dA(x)}{dx}=\frac{d}{d}\left ( \frac{x}{2}\sqrt{\frac{p^2}{4}-x^2} \right )=\frac{p^2-8x^2}{4\sqrt{-4x^2+p^2}}=0\to x=\frac{p\sqrt{2}}{4}\ \therefore \ y=\frac{p\sqrt{2}}{4}}\\\\\mathrm{Sendo\ x=y=\frac{p\sqrt{2}}{4}\ \therefore \ O\ quadril\acute{a}tero\ de\ maior\ \acute{a}rea\ \acute{e}\ um\ quadrado.}[/latex]

Nota: eu apelei para as derivadas pelo pouco tempo que tenho agora, mas dá para encontrar os maximizadores de A(x) sem derivadas. Logo mais eu posto.

A diagonal é o segmento AC, portanto é igual a 7. O resto parte da análise do seno de um ângulo (valor máximo 1). Os dois ângulos ali são iguais pois é um paralelogramo.

Poxa, não consigo concordar ainda com a sua resolução, pois em nenhum momento o enunciado afirma que o quadrilátero de área máxima é um losango tal como foi assumido na sua resolução (respeitosamente falando). Que foi a segunda pergunta que eu te fiz.

por **tales amaral** Sáb 05 Mar 2022, 17:52

Giovana Martins escreveu:
tales amaral escreveu:
Giovana Martins escreveu:
tales amaral escreveu:

A área é [latex]A = 2 \cdot \left(\dfrac{7\cdot 7 \cdot \text{sen} (x)}{2} \right )[/latex]. Seu valor máximo ocorre quando sen(x) = 1 e é dado por [latex]A = 2 \cdot \left(\dfrac{7\cdot 7 \cdot 1}{2} \right ) = 49[/latex].

Tales, estou meio enferrujada em geometria plana. O que garante que a diagonal do quadrilátero vale 7? A propósito, ainda que esteja correto o valor da diagonal, respeitosamente, a sua resolução me parece um tanto equivocada. Como garantimos que o quadrilátero de maior área é de fato um losango? Na minha resolução eu parti de um quadrilátero genérico até concluir que o quadrilátero de área máxima é um quadrado ao invés de um losango.

Digamos que eu tivesse partido da suposição de que o losango, ao invés de um retângulo como eu fiz inicialmente, fosse o quadrilátero de maior área:

[latex]\\\mathrm{Seja\ o\ quadril\acute{a}tero\ de\ diagonais\ x\ e\ y\ e\ p\ o\ perimetro\ do\ quadril\acute{a}tero.}\\\\\mathrm{Logo, \frac{p}{4}=\frac{1}{2}\sqrt{x^2+y^2}\ \therefore \ y=\sqrt{\frac{p^2}{4}-x^2}\ \therefore \ A(x,y)=\frac{xy}{2}=\frac{x}{2}\sqrt{\frac{p^2}{4}-x^2}=A(x)}\\\\\mathrm{\frac{dA(x)}{dx}=\frac{d}{d}\left ( \frac{x}{2}\sqrt{\frac{p^2}{4}-x^2} \right )=\frac{p^2-8x^2}{4\sqrt{-4x^2+p^2}}=0\to x=\frac{p\sqrt{2}}{4}\ \therefore \ y=\frac{p\sqrt{2}}{4}}\\\\\mathrm{Sendo\ x=y=\frac{p\sqrt{2}}{4}\ \therefore \ O\ quadril\acute{a}tero\ de\ maior\ \acute{a}rea\ \acute{e}\ um\ quadrado.}[/latex]

Nota: eu apelei para as derivadas pelo pouco tempo que tenho agora, mas dá para encontrar os maximizadores de A(x) sem derivadas. Logo mais eu posto.

A diagonal é o segmento AC, portanto é igual a 7. O resto parte da análise do seno de um ângulo (valor máximo 1). Os dois ângulos ali são iguais pois é um paralelogramo.

Poxa, não consigo concordar ainda com a sua resolução, pois em nenhum momento o enunciado afirma que o quadrilátero de área máxima é um paralelogramo tal como foi assumido na sua resolução (respeitosamente falando). Que foi a segunda pergunta que eu te fiz.

"Dentre todos os paralelogramos ABCD com AB=AC=7". A questão fala que ABCD é um paralelogramo. O resto parte disso.

por **Giovana Martins** Sáb 05 Mar 2022, 18:01

Opa, editei a minha pergunta na postagem anterior. Onde estava paralelogramo leia-se losango. O enunciado não fala qual de qual paralelogramo se trata. Ao meu ver isso tem de ser decifrado ao longo da resolução.

"Poxa, não consigo concordar ainda com a sua resolução, pois em nenhum momento o enunciado afirma que o quadrilátero de área máxima é um losango tal como foi assumido na sua resolução (respeitosamente falando). Que foi a segunda pergunta que eu te fiz.
"