SAS - Geometria plana

por Bruna Lourenci Qui 03 Mar 2022, 12:38

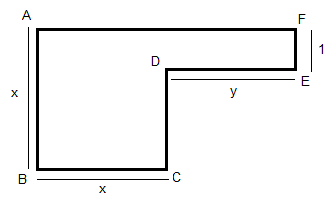
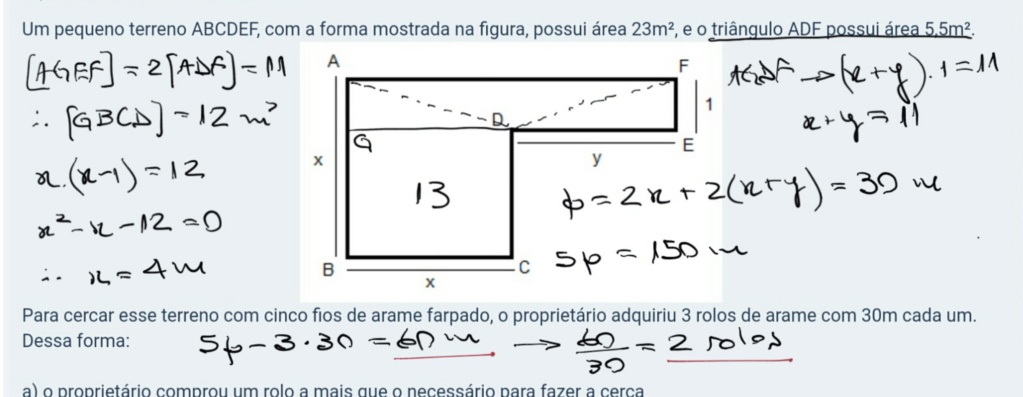
Um pequeno terreno ABCDEF, com a forma mostrada na figura, possui área 23m², e o triângulo ADF possui área 5,5m².

Para cercar esse terreno com cinco fios de arame farpado, o proprietário adquiriu 3 rolos de arame com 30m cada um. Dessa forma:

a) o proprietário comprou um rolo a mais que o necessário para fazer a cerca

b) o proprietário deve comprar um rolo a mais, pois precisa de mais 15m para completar a cerca

c) o proprietário deve comprar um rolo a mais, pois precisa de mais 25m para completar a cerca

d) o proprietário deve comprar dois rolos a mais, pois precisa de mais 55m para completar a cerca

e) o proprietário deve comprar dois rolos a mais, pois precisa de mais 60m para completar a cerca

Gabarito: E) o proprietário deve comprar dois rolos a mais, pois precisa de mais 60m para completar a cerca

Preciso de ajuda. Eu sei que fiz alguma coisa errada na minha conta, porque encontrei uma incongruência no meu cálculo. Gostaria de saber o que eu fiz de errado e qual a maneira correta de resolver a questão.

Vou mostrar como fiz: primeiro separei a figura em um quadrado de lado x e em um retângulo de lados y e 1. A área de do quadrado (x²) mais a área do retângulo (y.1) deve ser igual a área total do terreno, que é 23m². Depois, substitui na fórmula da área do triângulo as informações que eu tinha, no caso a base deveria ser x+y, portanto A=(x+y).1/2 = 5,5m².

Sabendo disso, eu utilizei a área do triângulo ADF para descobrir que x = 11 - y. Dessa forma, substitui o x na hora de calcular a área total, ficando assim: A = (11 - y)² + y = 23. Acabei caindo em uma bhaskara e encontrei como valor positivo de y 10,5.

Essa é a parte em que descubro uma incongruência: quando eu substitui o y na área total, encontrei que x = 3,5, mas quando substitui o x na área do triângulo, encontrei que x = 0,5.

Tentei continuar a conta considerando que x = 3,5 e cheguei ao resultado de que ainda seriam precisos mais 85m de arame, portanto o proprietário precisaria de mais 3 rolos de arame.

Acontece que não encontrei isso em nenhuma opção e devido a incongruência que encontrei tenho certeza de que errei alguma coisa, mas já revi minhas contas várias vezes e não consigo encontrar o erro.

Alguém pode me ajudar, por favor? Sad

por **qedpetrich** Qui 03 Mar 2022, 12:52

Olá Bruna;

Na verdade o seu erro se encontra a partir da resolução das raízes da expressão quadrática, veja:

$SAS - Geometria plana Png$

Tente prosseguir agora.

por Bruna Lourenci Sex 04 Mar 2022, 00:08

qedpetrich escreveu:Olá Bruna;

Na verdade o seu erro se encontra a partir da resolução das raízes da expressão quadrática, veja:

$SAS - Geometria plana Png$

Tente prosseguir agora.

Nossa, me esqueci completamente do produto notável! affraid