Determine m para que a equação do 2º grau tenha...
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Determine m para que a equação do 2º grau tenha...
Determine m para que a equação do 2º grau tenha...
Boa tarde ! Estou tentando resolver a seguinte questão, mas não estou chegando a resposta do gabarito. Alguém pode me ajudar ?
Determine m para que a equação do 2º grau mx²-2(m-1)x-m-1=0 tenha uma única raiz entre -1 e 2.
Gabarito: m < 3/2 e m ≠ 0 e m > 3.
Minha resposta foi 3/2 < m < 3 e m ≠ 0.
Fiz x < 2 que deu 0 < m < 3 depois fiz x > -1 que deu m<0 e m>3/2, por último fiz Δ = 0 que deu m ≠ 0, aí fiz a interseção chegando a 3/2 < m < 3 e m ≠ 0.
O gabarito está mesmo correto ?
Determine m para que a equação do 2º grau mx²-2(m-1)x-m-1=0 tenha uma única raiz entre -1 e 2.
Gabarito: m < 3/2 e m ≠ 0 e m > 3.
Minha resposta foi 3/2 < m < 3 e m ≠ 0.
Fiz x < 2 que deu 0 < m < 3 depois fiz x > -1 que deu m<0 e m>3/2, por último fiz Δ = 0 que deu m ≠ 0, aí fiz a interseção chegando a 3/2 < m < 3 e m ≠ 0.
O gabarito está mesmo correto ?
BiaBeatriz- Iniciante
- Mensagens : 25
Data de inscrição : 23/03/2021
 Re: Determine m para que a equação do 2º grau tenha...
Re: Determine m para que a equação do 2º grau tenha...
São possíveis três casos.
I) Duas raízes reais distintas com - 1 entre as raízes;
II) Duas raízes reais distintas com 2 entre as raízes;
III) Uma única raiz real com - 1 pela esquerda e 2 pela direita da raiz.
Encontremos os valores para cada caso:
i) f(-1) = m + 2m - 2 - m - 1
f(-1) = 2m - 3
Logo:
m.(2m - 3) < 0
0 < m < 3/2
ii) f(2) = 4m - 4m + 4 - m - 1
f(2) = 3 - m
Logo:
m.(3 - m) < 0
m < 0 ou m > 3
III) ∆ = 0
∆ = (- 2m + 2)² - 4.m(-m - 1)
∆ = 4 - 8m + 4m² + 4m² + 4 m
∆ = 8m² - 4m + 4
S = Ø (a possibilidade de raiz única não existe, então nem precisamos verificar as condições para que -1 esteja pela esquerda e 2 pela direita).
Por fim, m ≠ 0 é condição para que a equação seja do 2º grau.
A solução do problema é a união das três possibilidades, isto é:
S = m < 3/2 ou m > 3 e m ≠ 0.
I) Duas raízes reais distintas com - 1 entre as raízes;
II) Duas raízes reais distintas com 2 entre as raízes;
III) Uma única raiz real com - 1 pela esquerda e 2 pela direita da raiz.
Encontremos os valores para cada caso:
i) f(-1) = m + 2m - 2 - m - 1
f(-1) = 2m - 3
Logo:
m.(2m - 3) < 0
0 < m < 3/2
ii) f(2) = 4m - 4m + 4 - m - 1
f(2) = 3 - m
Logo:
m.(3 - m) < 0
m < 0 ou m > 3
III) ∆ = 0
∆ = (- 2m + 2)² - 4.m(-m - 1)
∆ = 4 - 8m + 4m² + 4m² + 4 m
∆ = 8m² - 4m + 4
S = Ø (a possibilidade de raiz única não existe, então nem precisamos verificar as condições para que -1 esteja pela esquerda e 2 pela direita).
Por fim, m ≠ 0 é condição para que a equação seja do 2º grau.
A solução do problema é a união das três possibilidades, isto é:
S = m < 3/2 ou m > 3 e m ≠ 0.
Rory Gilmore- Monitor

- Mensagens : 1878
Data de inscrição : 28/05/2019
Localização : Yale University - New Haven, Connecticut
won gosta desta mensagem
 Re: Determine m para que a equação do 2º grau tenha...
Re: Determine m para que a equação do 2º grau tenha...
acredito que o gabarito esteja incorreto. acho que vc interpretou o passo-a-passo da questão de maneira incorreta.
para que haja uma única raiz entre -1 e 2, podem ocorrer duas ocasiões distintas:
1)
-1 0 = m<0 ou m> 3/2
b) -1<-b/2a = m>0 ou m>1/2
c) a.f(2) <0 = m<0 ou m>3
fazendo a intersecção de todos os 3 casos, temos: m<0 ou m>3
2)
a) a.f(2) >0 = 0-b/2a = m<-1 ou m>0
c) a.f(-1) <0 = 03 ou 0
para que haja uma única raiz entre -1 e 2, podem ocorrer duas ocasiões distintas:
1)
-1 0 = m<0 ou m> 3/2
b) -1<-b/2a = m>0 ou m>1/2
c) a.f(2) <0 = m<0 ou m>3
fazendo a intersecção de todos os 3 casos, temos: m<0 ou m>3
2)
a) a.f(2) >0 = 0-b/2a = m<-1 ou m>0
c) a.f(-1) <0 = 03 ou 0

caique farias- Iniciante
- Mensagens : 30
Data de inscrição : 04/08/2022
Rory Gilmore gosta desta mensagem
 Re: Determine m para que a equação do 2º grau tenha...
Re: Determine m para que a equação do 2º grau tenha...
Olá, eu não entendi o que você quis dizer, mas não há erro na resolução anterior e no gabarito.
Como vemos na imagem abaixo, ocorrem três possibilidades:
i) Duas raízes, sendo uma à esquerda de - 1 e outra entre -1 e 2.
Nesse caso devemos ter:
∆ > 0 e a.f(-1) < 0 e a.f(2) > 0
Como o discriminante é sempre positivo, analisamos a.f(-1) < 0 e a.f(2) > 0 e obtemos a solução (em negrito).
0 < m < 3/2
0 < m < 3
0 < m < 3/2
ii) Duas raízes, sendo uma à direita de 2 e outra entre -1 e 2.
Nesse caso devemos ter:
∆ > 0 e a.f(2) < 0 e a.f(-1) > 0
m < 0 ou m > 3
m < 0 ou m > 3/2
m < 0 ou m > 3
iii) Uma única raiz entre - 1 e 2.
Nesse caso devemos ter:
∆ = 0 e a.f(-1) > 0 e a.f(2) > 0.
Que é impossível, pois o discriminante é sempre positivo.
A solução final é a união de todas as possibilidades, ou seja, S = m < 3/2 ou m > 3 e m ≠ 0.
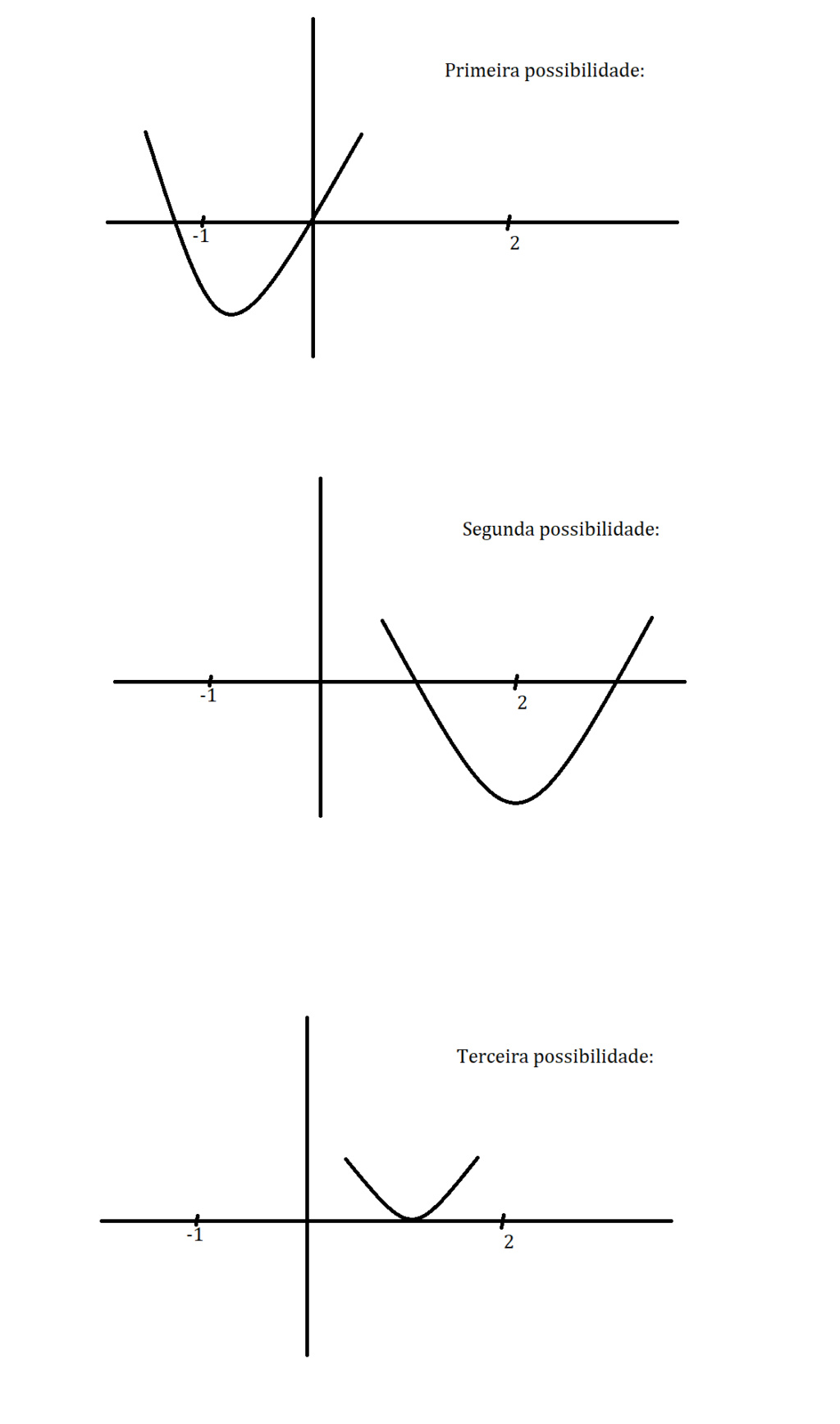
Como vemos na imagem abaixo, ocorrem três possibilidades:
i) Duas raízes, sendo uma à esquerda de - 1 e outra entre -1 e 2.
Nesse caso devemos ter:
∆ > 0 e a.f(-1) < 0 e a.f(2) > 0
Como o discriminante é sempre positivo, analisamos a.f(-1) < 0 e a.f(2) > 0 e obtemos a solução (em negrito).
0 < m < 3/2
0 < m < 3
0 < m < 3/2
ii) Duas raízes, sendo uma à direita de 2 e outra entre -1 e 2.
Nesse caso devemos ter:
∆ > 0 e a.f(2) < 0 e a.f(-1) > 0
m < 0 ou m > 3
m < 0 ou m > 3/2
m < 0 ou m > 3
iii) Uma única raiz entre - 1 e 2.
Nesse caso devemos ter:
∆ = 0 e a.f(-1) > 0 e a.f(2) > 0.
Que é impossível, pois o discriminante é sempre positivo.
A solução final é a união de todas as possibilidades, ou seja, S = m < 3/2 ou m > 3 e m ≠ 0.

Rory Gilmore- Monitor

- Mensagens : 1878
Data de inscrição : 28/05/2019
Localização : Yale University - New Haven, Connecticut
 Re: Determine m para que a equação do 2º grau tenha...
Re: Determine m para que a equação do 2º grau tenha...
obrigado pela correção! acredito que meu erro tenha sido não unir as soluções.

caique farias- Iniciante
- Mensagens : 30
Data de inscrição : 04/08/2022
Rory Gilmore gosta desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» Determine m para que se tenha para todo x ∈ R
» POLINOMIOS Determine a, b, c de modo que se tenha para
» Determine m para que se tenha para ∀ x ∈ ℝ:
» Determine m para que se tenha para ∀ x ∈ ℝ:
» Determine m para que se tenha para ∀ x ∈ IR :
» POLINOMIOS Determine a, b, c de modo que se tenha para
» Determine m para que se tenha para ∀ x ∈ ℝ:
» Determine m para que se tenha para ∀ x ∈ ℝ:
» Determine m para que se tenha para ∀ x ∈ IR :
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












