Geometria Euclidiana Plana

por William Minerva Seg 07 Fev 2022, 12:41

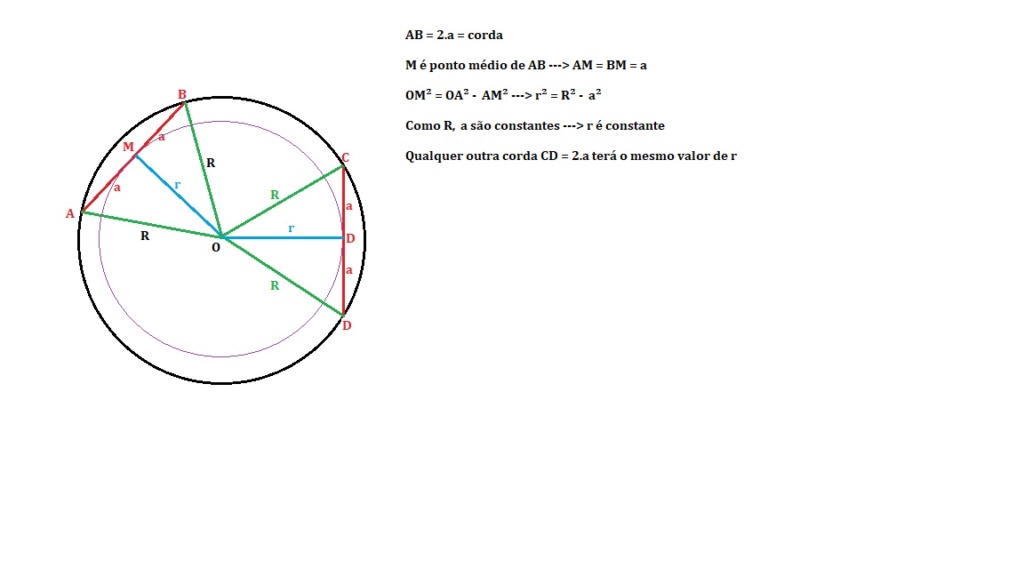
Mostre que os pontos médios de todas as cordas congruentes de uma circunferência qualquer estão em uma circunferência concêntrica com a original e com raio igual à distância de uma corda ao centro; Mostre também que as cordas são todas tangentes a esta circunferência interior. Desconsidere os diâmetros.

Alguém pode me ajudar por favor? Não entendi como eu faço para mostrar isso...

por **Rory Gilmore** Seg 07 Fev 2022, 13:06

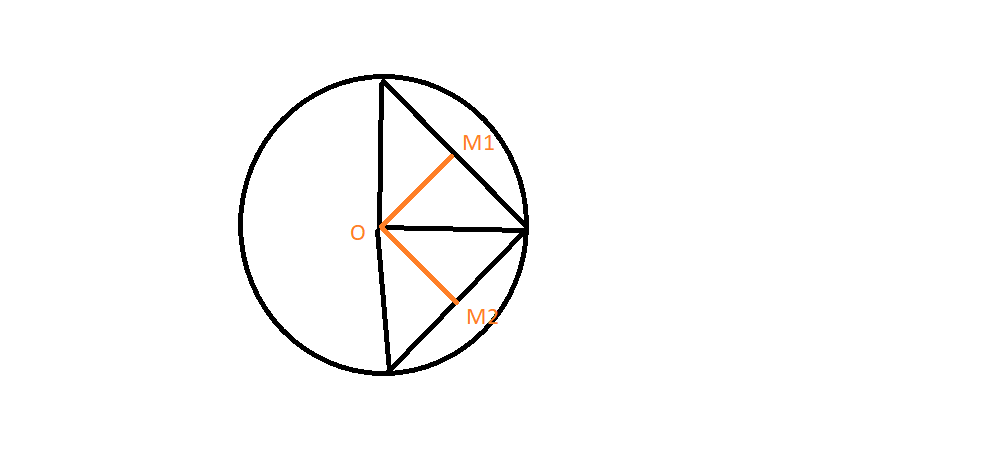
Se O é o centro da circunferência dada e M1, M2, M3, ..., Mn são os respectivos pontos médios das n cordas congruentes, logo OM1, OM2, OM3, ..., OMn são todos perpendiculares a tais cordas e têm medidas iguais (por congruência de triângulos), logo, tem uma circunferência com tal raio passando por todos esses pontos e de mesmo centro O.

A parte da tangência eu deixo para você tentar.