Volume do Sólido S

por nessinhanl Sáb 11 Dez 2021, 01:16

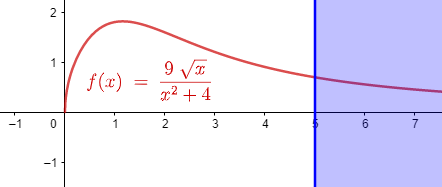
Considere a região infinita R que está sob a curva [latex]y=\frac{9\Large\sqrt{x}}{x^2+4}[/latex], acima do eixo x e à direita da reta x=5.

Mostre que pela rotação da região R ao redor do eixo x obtém-se um sólido S com volume finito.
Calcule o volume do sólido S.

por **Giovana Martins** Sáb 11 Dez 2021, 09:39

Creio que seja isso.

[latex]\\\mathrm{V=\int_{5}^{\infty }\pi \left ( \frac{9\sqrt{x}}{x^2+4} \right )^2dx=\pi \lim_{t\to \infty}\int_{5}^{t }\frac{81x}{(x^2+4)^2}dx}\\\\\mathrm{V=\int_{5}^{\infty }\pi \left ( \frac{9\sqrt{x}}{x^2+4} \right )^2dx=\pi \lim_{t\to \infty}\left [ \frac{81(t^2-25)}{58(t^2+4)} \right ]=\frac{81\pi }{58}<\infty}[/latex]

por nessinhanl Sáb 11 Dez 2021, 10:26

Giovana Martins escreveu:
Creio que seja isso.

[latex]\\\mathrm{V=\int_{5}^{\infty }\pi \left ( \frac{9\sqrt{x}}{x^2+4} \right )^2dx=\pi \lim_{t\to \infty}\int_{5}^{t }\frac{18x}{(x^2+4)^2}dx}\\\\\mathrm{V=\int_{5}^{\infty }\pi \left ( \frac{9\sqrt{x}}{x^2+4} \right )^2dx=\pi \lim_{t\to \infty}\left [ 9\left ( -\frac{1}{4+t^2}+\frac{1}{29} \right ) \right ]=\frac{9\pi }{29}<\infty}[/latex]

Giovana, segue o gabarito que o professor acabou de divulgar. Poderia ter algum erro no gabarito ou realmente está correto já que você chegou em outra resposta?

Usando o método dos discos:

[latex]\Large V(\Large S)=\pi\int_{5}^{\infty}R^{2}(x)dx=\lim_{T \to \infty}\pi\int_{5}^{T} R^{2}(x)dx=\lim_{T \to \infty}\Large V(\Large S_{T})[/latex]

em que [latex]R(x)=\frac{9\sqrt{x}}{x^2+4}[/latex]

[latex]\Large V(\Large S_{T})=\pi\int_{5}^{T}\left[\left(\frac{9\sqrt{x}}{x^2+4}\right)^2\right]dx[/latex]

[latex]=\pi\int_{5}^{T}\left(\frac{81x}{(x^2+4)^2}\right)dx=\frac{81\pi }{2}\int_{5}^{T}\left(\frac{2x}{(x^2+4)^2}\right)dx=\left[-\frac{81\pi}{2(x^2+4)}\right]_{5}^{T}[/latex]

[latex]\Large V(\Large S_{T})=\frac{81\pi}{2}\left(\frac{1}{(5^2+4)}-\frac{1}{ (T^2+4)}\right)[/latex]

logo

[latex]\Large V(\Large S)=\lim_{T \to \infty}\Large V(\Large S_{T})=\frac{81\pi}{2}.\lim_{T \to \infty}\left(\frac{1}{(5^2+4)}-\frac{1}{ (T^2+4)}\right)=\frac{81\pi}{58}=4,3873966369099[/latex]

por **Giovana Martins** Sáb 11 Dez 2021, 10:34

vanessa (suponho que seu nome seja Vanessa), está certinho o que o seu professor fez. Note que sem querer eu disse que 9²=18 por conta de um erro de digitação. Nisso o resultado ficou ligeiramente diferente, mas ajustando isso, o meu resultado chega exatamente no do seu professor.

por Conteúdo patrocinado

Volume do Sólido S

Volume do Sólido S

Re: Volume do Sólido S

Re: Volume do Sólido S

Re: Volume do Sólido S

Re: Volume do Sólido S

Um fórum livre e democrático.