geometria plana

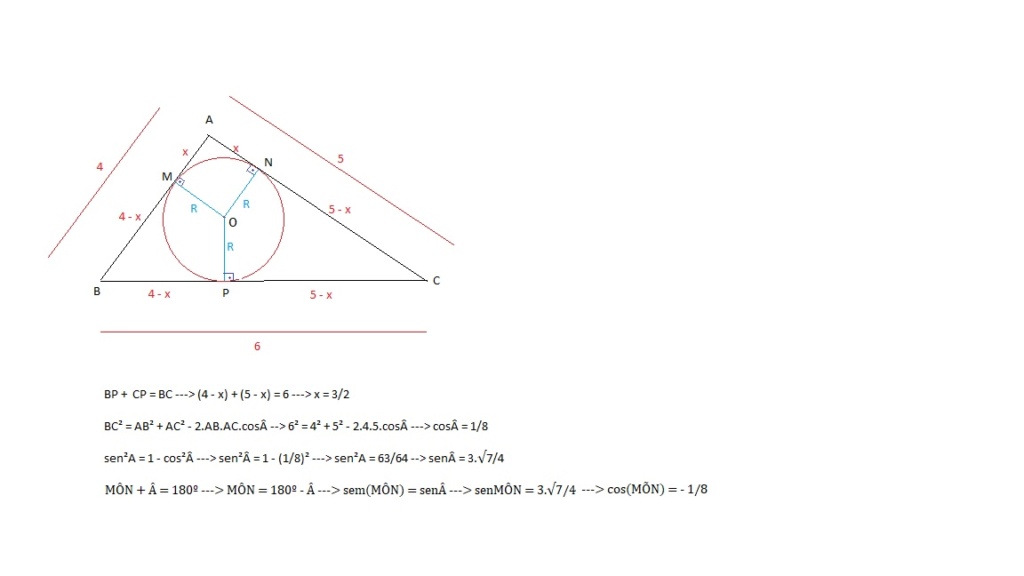
Determine o raio da circunferência circunscrita ao triângulo de lados que medem 4 cm, 5 cm e 6 cm.

Uma figura para ajudar:

continuando a resolução do Élcio...




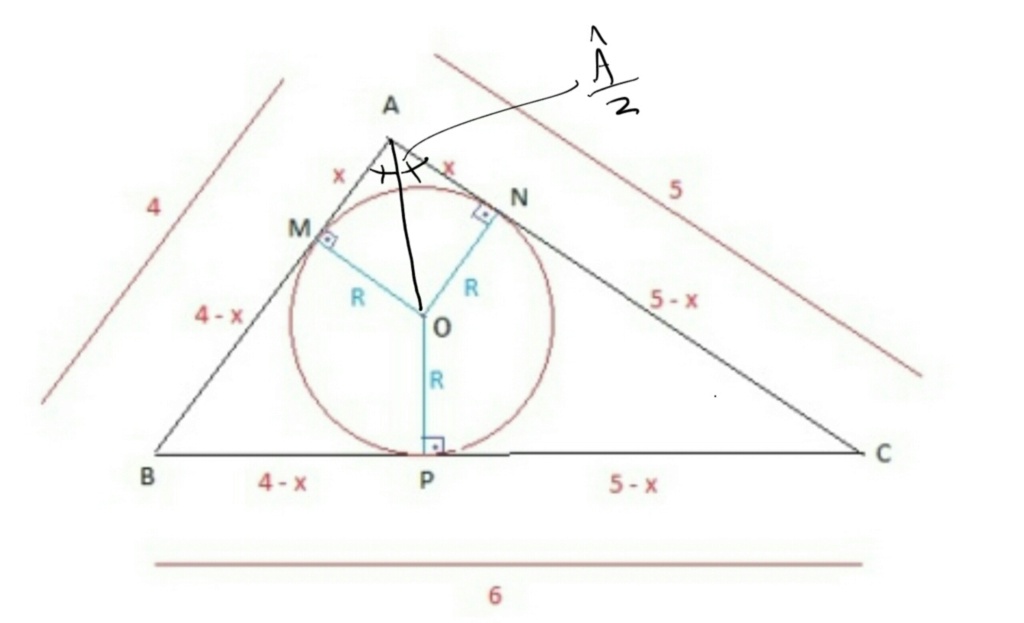
cos = 1/8
---> cos(Â/2) = [latex]\sqrt{\frac{1+cosA}{2}} = \sqrt{\frac{1+\frac{1}{8}}{2}} = \sqrt{\frac{9}{16}} = \frac{3}{4}[/latex]

---> sen(Â/2) = [latex]\sqrt{\frac{1-cosA}{2}} = \sqrt{\frac{1-\frac{1}{8}}{2}} = \sqrt{\frac{7}{16}} = \frac{\sqrt{7}}{4}[/latex]

.:. tg(Â/2) = √7/3

tg(Â/2) = R/x -----> R = x.tg(Â/2) = (3/2).√7/3 ----->R = √7/2 =˜ 1,3 cm

porém, se o enunciado queria dizer a circunferência que circunscreve o triângulo...

S = 4.5.6/(4R) -----> R = 5.6/S

p = (4 + 5 + 6)/2 = 15/2
p - 4 = 7/2
p - 5 = 5/2
p - 6 = 3/2
[latex]\\S= \sqrt{\frac{15}{2}.\frac{7}{2}.\frac{5}{2}.\frac{3}{2}} = \frac{1}{4}\cdot\sqrt{3.5.7.5.3}=\frac{15}{4}\sqrt{7}[/latex]

.:. R = 5.6/(15√7/4) = 4.5.6/(15√7) = 8/√7 -----> R = 8√7/7 =˜ 3,02 cm

Boa noite, obrigada pela resposta, é essa última que mandou que a questão quer, mas estou em dúvida (estou fraca nessa matéria rs). Preciso ir direto com a sua resolução com a circunferência que circunscreve o triângulo?? ou preciso iniciar com o que o Élcio enviou e posteriormente a sua?

Alethea

1)
observe que editei minha segunda resposta para corrigir a aproximação do valor de R. Fiz isto para ficar claro que a lado 6 do triângulo NÃO é diâmetro da circunferência, é um pouco menor.

2)
Quanto a sua pergunta, a decisão é sua. Foi você quem interpretou o que a questão quer, então responda a questão; eu tive dificuldade nessa interpretação mas acho que é a minha segunda resposta.

3)
Se você "está fraca nessa matéria", então não entendeu/conhece a fórmula que usei e relaciona a área do triângulo com o raio da circunf. circunscrita, e nem que usei o teorema de Heron para calcular a área do triângulo. Sugiro perquisar na internet por:
- raio da circunferência circunscrita ao triângulo;
- teorema de Heron.
Aproveite e pesquise também sobre o teorema de Brahmagupta, do qual o teor. de Heron é um caso particular.