Ângulo formado por 2 planos
4 participantes
Página 1 de 1
 Re: Ângulo formado por 2 planos
Re: Ângulo formado por 2 planos
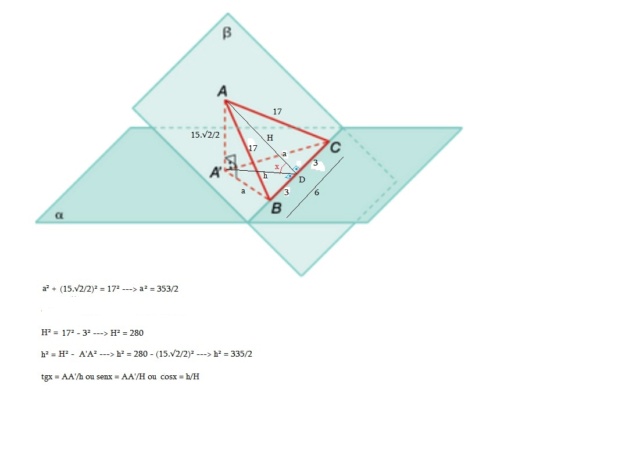
Dante,dantecamara escreveu:A figura abaixo mostra 2 planos secantes, α e β e os pontos A, B,C e A' tais que {C,B,A'} ⊂ α, A ∈ β e A não pertence a α e A' é a projeção ortogonal de A sobre α. Sabe-se que AB=AC=17cm , BC = 6cm r AA' = 15V2/2 cm
Calcule a medida x de um ângulo agudo formado pelos planos α e β
- Resposta:
com esses números não encontrei um ângulo de 45°, apenas de 40°.


Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR

Elcioschin- Grande Mestre

- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Ângulo formado por 2 planos
Re: Ângulo formado por 2 planos
Oi dantecamara! 
Acredito que o enunciado esteja incorreto. Para encontrar o gabarito, o certo seria BC = 16 cm.
Deixo minha resposta como complemento da resposta dos mestres (só para não perder a viagem kkkkk)
Pelo Teorema das três perpendiculares podemos desenhar um ponto P tal que AA'P= APC = 90o. Veja a figura:
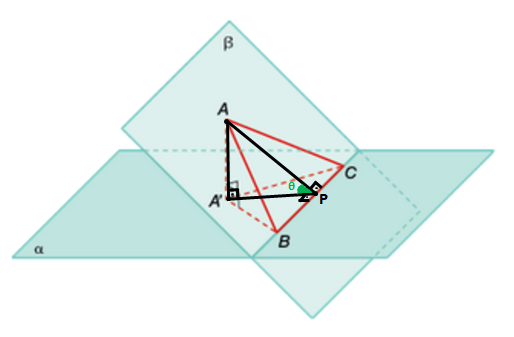
Veja que AP é a altura do triângulo isósceles ABC. Portanto, olhando para o triângulo retângulo APC:
[latex]\\\left\{\begin{matrix} PC=\frac{BC}{2}=8\\ AC = 17\\ AP^2 + PC^2 = AC^2 \end{matrix}\right.\;\rightarrow\;AP=15[/latex]
Agora que temos AA' e AP podemos encontrar o ângulo entre os planos APA'=θ.
Olhando para o triângulo retângulo AA'P:
[latex]\\sen\theta = \frac{AA'}{AP}=\frac{\frac{\cancel{15}\sqrt{2}}{2}}{\cancel{15}}=\frac{\sqrt{2}}{2}\;,\;\;\;0\leq \theta\leq 90^o\\\\ \rightarrow\;\;\boxed{\theta = 45^o}[/latex]

Acredito que o enunciado esteja incorreto. Para encontrar o gabarito, o certo seria BC = 16 cm.
Deixo minha resposta como complemento da resposta dos mestres (só para não perder a viagem kkkkk)
Pelo Teorema das três perpendiculares podemos desenhar um ponto P tal que AA'P= APC = 90o. Veja a figura:

Veja que AP é a altura do triângulo isósceles ABC. Portanto, olhando para o triângulo retângulo APC:
[latex]\\\left\{\begin{matrix} PC=\frac{BC}{2}=8\\ AC = 17\\ AP^2 + PC^2 = AC^2 \end{matrix}\right.\;\rightarrow\;AP=15[/latex]
Agora que temos AA' e AP podemos encontrar o ângulo entre os planos APA'=θ.
Olhando para o triângulo retângulo AA'P:
[latex]\\sen\theta = \frac{AA'}{AP}=\frac{\frac{\cancel{15}\sqrt{2}}{2}}{\cancel{15}}=\frac{\sqrt{2}}{2}\;,\;\;\;0\leq \theta\leq 90^o\\\\ \rightarrow\;\;\boxed{\theta = 45^o}[/latex]

Victor011- Fera

- Mensagens : 663
Data de inscrição : 21/10/2015
Idade : 26
Localização : Rio de Janeiro, Brasil
Medeiros gosta desta mensagem
 Re: Ângulo formado por 2 planos
Re: Ângulo formado por 2 planos
matou a pau, Victor! Também achava que o erro estava no enunciado mas não tive a iniciativa de procurar o conserto.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Victor011 gosta desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» o ângulo formado pela bissetriz do ângulo interno A com a mediatriz do lado BC mede:
» ângulo formado p/ bissetriz
» ( PUC - SP ) ângulo formado ... !??
» Ângulo formado.
» Ângulo formado por cordas
» ângulo formado p/ bissetriz
» ( PUC - SP ) ângulo formado ... !??
» Ângulo formado.
» Ângulo formado por cordas
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos