Olimpíada Canguru - Áreas

Seis perpendiculares foram desenhadas a partir dos pontos médios dos lados de um triângulo equilátero, conforme mostrado na figura. Que fração da área do triângulo é a área do hexágono cinzento delimitado por essas perpendiculares?

a)1/3
b)2/5
c)4/9
d)1/2
e)3/2

Gabarito:

Fala, meu consagrado! Tudo certo?

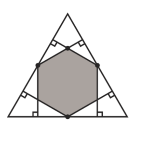
Observe que o centro do hexágono está no baricentro do triângulo.

Logo, o lado do hexágono é:



Onde h é a altura do triângulo equilátero.
Desse modo:

 (l é o lado do triângulo)
Assim, a área do hexágono e a do triângulo são:

Área do hexágono:





Área do triângulo:



Concluindo:



Espero ter ajudado! Grande Abraço!

Obrigado pela resolução,ótimo raciocínio!

Eu tinha feito da seguinte forma,errei somente na fórmula trigonométrica da área. Fica aqui disponível para quem se interessar:



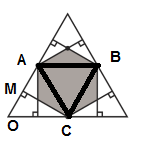
Como OC e OA são os pontos médios dos lados do triângulo maior,o triângulo OAC é isósceles. Como o ângulo distinto deste mede 60º,concluimos que se trata de um triângulo equilátero de lado L/2,tomando L como o lado do triângulo maior.

O segmento MC é altura de AOC e coincide com a bissetriz de ACO. Logo,[latex]\widehat{ACO}[/latex]mede 30º

Tomando a como o lado do hexágono,fazendo Lei dos cossenos em um dos triângulos menores:

[latex]\frac{L^^{2}}{4} = a^^{2} + a^^{2} - 2.a^^{2}cos 120^{\circ}[/latex]


Logo,a² = L²/12

[latex]A_{Hex} = \frac{L^^{2}\sqrt{3}}{4.4} + 3\frac{a^^{2}\sqrt{3}}{2}.\frac{1}{2}[/latex]


Para os triângulos menores utilizei a fórmula trigonométrica da área.

[latex]A_{Hex} = \frac{L^^{2}\sqrt{3}}{8}[/latex]


e

[latex]A_{Tr} = \frac{L^^{2}\sqrt{3}}{4}[/latex]