simulado sas

Uma família possui um balanço afixado por cordas
de 1,5 metro em uma estrutura que está a 2 metros do
chão em um quarto fechado, como na imagem.

O ângulo de balanço vai de uma parede à outra, e
os pais, preocupados com a segurança dos filhos que
brincam no balanço, decidiram recriar o modelo de modo
que a aceleração do balanço diminuísse. Para isso, eles
concluíram que bastaria modificar a altura da estrutura e
aumentar o tamanho das cordas até diminuir à metade o
ângulo de balanço. Porém, desejam conservar os pontos
A e B extremos da trajetória determinada pelo balanço.
A altura da estrutura, em metro, deverá ser

a)1,5
b)2,0
c)3,0
d)3,5
e)4,0


Resposta: D

Bom dia!

  Como a questão quer que o ângulo inicial seja reduzido à sua metade e que os pontos A e B sejam conservados, acontece esse caso da circunferência: 


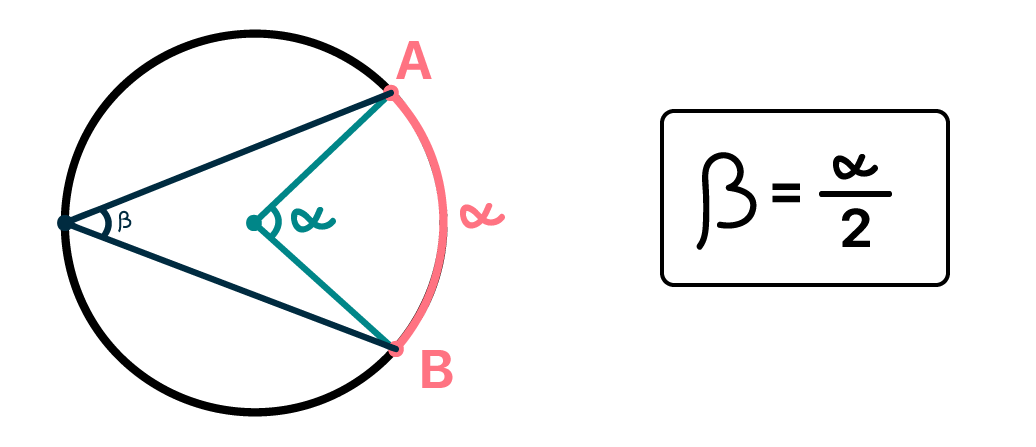
  Portanto, perceba que, juntando a nova altura com a inicial, achamos o diâmetro da circunferência. Para achar o seu valor, devemos notar que as cordas, no primeiro momento, atingiam o centro da figura, ou seja, descreviam o raio. Logo, para achar o diâmetro, devemos só acrescer 1,5 m:


  Assim, somando a altura inicial, 2m, com o acréscimo de 1,5m= 3,5m.

  (A soma das alturas não é igual ao diâmetro porque o brinquedo está 0,5 m acima do solo)

  Se tiver ficado confuso, é só avisar.

Excelente sacada, Fernanda!