Matemática - Geometria Plana e Espacial - UP 2018
3 participantes
Página 1 de 1
Matemática - Geometria Plana e Espacial - UP 2018
por Artur Bensch Borst Qua 23 Jun 2021, 09:48
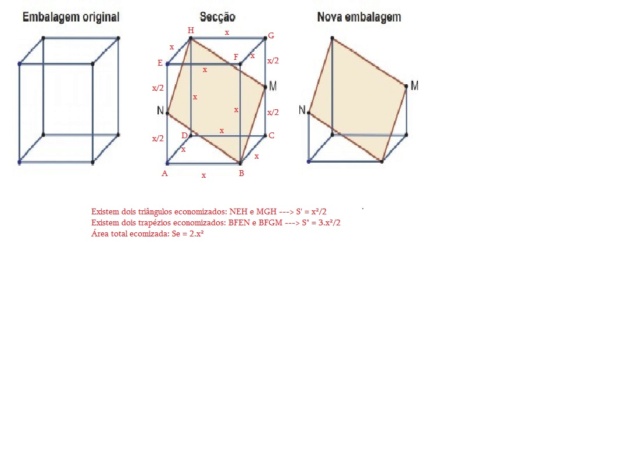
Depois de alguns estudos, uma empresa observou que poderia apresentar seus produtos em embalagens mais baratas que a utilizada até então. A embalagem utilizada era um cubo de aresta x, enquanto a nova embalagem é obtida a partir da secção abaixo:
O valor que mais se aproxima da redução do papel a ser utilizado na nova embalagem em comparação à anterior é:
a)20%.
b)30%.
c)50%.
d)70%.
e)80%.
[Resposta:][/b)]
Tive dificuldades para chegar na resposta correta, como posso encontrá-la? Desde já agradeço.
O valor que mais se aproxima da redução do papel a ser utilizado na nova embalagem em comparação à anterior é:
a)20%.
b)30%.
c)50%.
d)70%.
e)80%.
[Resposta:][/b)]
Tive dificuldades para chegar na resposta correta, como posso encontrá-la? Desde já agradeço.
Última edição por Artur Bensch Borst em Qua 23 Jun 2021, 18:24, editado 1 vez(es)
Artur Bensch Borst- Iniciante
- Mensagens : 9
Data de inscrição : 21/06/2021
Re: Matemática - Geometria Plana e Espacial - UP 2018
por Elcioschin Qua 23 Jun 2021, 12:25
Não ficou claro se a embalagem tem ou não tem tampa.
De qualquer forma, eis um desenho para facilitar os cálculos:
De qualquer forma, eis um desenho para facilitar os cálculos:
Elcioschin- Grande Mestre
- Mensagens : 73186
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Matemática - Geometria Plana e Espacial - UP 2018
por jopagliarin Sex 11 Fev 2022, 18:50
Está correto assim?
jopagliarin- Jedi
- Mensagens : 399
Data de inscrição : 13/10/2019
Idade : 22
Localização : Curitiba/PR \\ Joaçaba/SC
Re: Matemática - Geometria Plana e Espacial - UP 2018
por Elcioschin Sex 11 Fev 2022, 19:39
As áreas dos trapézios e dos triângulos são áreas economizadas (áreas a serem abatidas da área original 6.x²)
Você colocou a área da tampa EFGH (x²) como economizada (também devem ser abatidas)
Logo você deverá considerar a nova "tampa" BMHN como existente, isto é ela deverá ser adicionada
Assim, não podemos somar áreas abatidas (- x²/2 - 3.x²/2 - x²) com a área + 5.x²/4
O correto deve ser:
Nova área = 6.x² - (x²/2 + 3.x²/2 + x²) + 5.x²/4 = (17/4).x²
(17/4).x²/6.x² = (17/24).x² ~= 0,70 --> 70 % ---> Redução = 30 %
Você colocou a área da tampa EFGH (x²) como economizada (também devem ser abatidas)
Logo você deverá considerar a nova "tampa" BMHN como existente, isto é ela deverá ser adicionada
Assim, não podemos somar áreas abatidas (- x²/2 - 3.x²/2 - x²) com a área + 5.x²/4
O correto deve ser:
Nova área = 6.x² - (x²/2 + 3.x²/2 + x²) + 5.x²/4 = (17/4).x²
(17/4).x²/6.x² = (17/24).x² ~= 0,70 --> 70 % ---> Redução = 30 %
Elcioschin- Grande Mestre
- Mensagens : 73186
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tópicos semelhantes» Matemática - Geometria Plana e Espacial - UP 2018
» Matemática - Geometria Plana e Espacial - UP 2017
» Geometria espacial (UESB 2018)
» Geometria espacial - ENEM 2018
» IFRJ 2018 - Geometria plana
» Matemática - Geometria Plana e Espacial - UP 2017
» Geometria espacial (UESB 2018)
» Geometria espacial - ENEM 2018
» IFRJ 2018 - Geometria plana
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
