Divisão de Polinômios
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Divisão de Polinômios
por matheusbon Qui 10 Jun 2021, 17:29
Dando 
, o resto da divisão de 
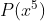por 
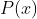é:
a)1
b)x^4+1
c)3
d)x^5+1
e)5
Gabarito: e
OBS: Há alguma forma de fazer essa questão sem ser dividindo "normalmente"?
a)1
b)x^4+1
c)3
d)x^5+1
e)5
Gabarito: e
OBS: Há alguma forma de fazer essa questão sem ser dividindo "normalmente"?
matheusbon- Padawan
- Mensagens : 56
Data de inscrição : 16/09/2020
Idade : 20
Localização : Brasil, Rio de Janeiro.
Re: Divisão de Polinômios
por Vitor Ahcor Sex 11 Jun 2021, 01:58
Olá,
Sabemos x5 - 1 = (x-1)*(x4+x3+x2+x+1)
⇒ x5 - 1 ≡ 0 mod P(x) ⇒ x5 ≡ 1 mod P(x)
Assim,
x20 ≡ 1 mod P(x)
x15 ≡ 1 mod P(x)
x10 ≡ 1 mod P(x)
x5 ≡ 1 mod P(x)
1 ≡ 1 mod P(x)
⇒ P(x5) ≡ 1+1+1+1+1 mod P(x)
Logo, o resto pedido é 5.
Sabemos x5 - 1 = (x-1)*(x4+x3+x2+x+1)
⇒ x5 - 1 ≡ 0 mod P(x) ⇒ x5 ≡ 1 mod P(x)
Assim,
x20 ≡ 1 mod P(x)
x15 ≡ 1 mod P(x)
x10 ≡ 1 mod P(x)
x5 ≡ 1 mod P(x)
1 ≡ 1 mod P(x)
⇒ P(x5) ≡ 1+1+1+1+1 mod P(x)
Logo, o resto pedido é 5.
____________________________________________
Cha-la head-cha-la
Vitor Ahcor- Monitor
- Mensagens : 780
Data de inscrição : 21/12/2018
Idade : 24
Localização : Taurdal
matheusbon gosta desta mensagem
Tópicos semelhantes» Divisao polinômios.
» Divisão de Polinômios
» Divisão de Polinômios 2
» Polinômios - (divisão)
» divisão de polinômios
» Divisão de Polinômios
» Divisão de Polinômios 2
» Polinômios - (divisão)
» divisão de polinômios
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
