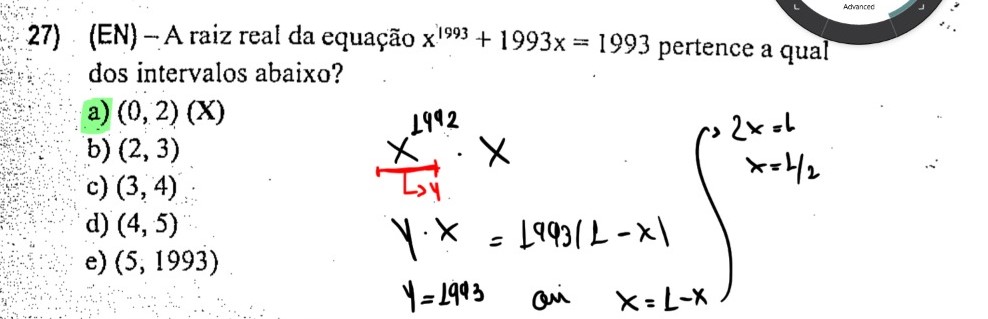EN-1993
4 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
natanlopes_17- Jedi

- Mensagens : 410
Data de inscrição : 14/07/2020
Idade : 21
Localização : Campinas, São Paulo
 Re: EN-1993
Re: EN-1993
Não, sua resolução está errada. (O que você fez dá um absurdo!)
Resolução
I)Defina,
f(x) = x^1993 + 1993x - 1993
Com isso, podemos dizer que a função f(x) é estritamente crescente, logo existe no máximo uma raiz real.
II)Agora observe que,
f(0) = -1993
f(2) = 2^1993 + 1993*2 - 1993 = 2^1993 + 1993
f(0)*f(2) < 0
Isso implica que sendo 'y' a raiz de f(x), temos:
y ∈ (0,2)
Resolução
I)Defina,
f(x) = x^1993 + 1993x - 1993
Com isso, podemos dizer que a função f(x) é estritamente crescente, logo existe no máximo uma raiz real.
II)Agora observe que,
f(0) = -1993
f(2) = 2^1993 + 1993*2 - 1993 = 2^1993 + 1993
f(0)*f(2) < 0
Isso implica que sendo 'y' a raiz de f(x), temos:
y ∈ (0,2)
Messias Castro- Recebeu o sabre de luz

- Mensagens : 105
Data de inscrição : 26/02/2021
Idade : 26
Localização : Fortaleza, CE
 Re: EN-1993
Re: EN-1993
Messias, não entendi o porquê f(0)*f(2) < 0 faz com que o 0 e 2 sejam intervalos da função. É uma propriedade?

eumilenalmeida- Iniciante
- Mensagens : 9
Data de inscrição : 14/02/2021
Idade : 22
Localização : São Pedro da Aldeia - RJ
 Re: EN-1993
Re: EN-1993
Para x = 0 a função é negativa (abaixo do eixo x)
Para x = 2 a função é positiva (acima do eixo x)
Em algum lugar entre 0 e 2 o gráfico da função vai cortar o eixo x ---> é a raiz
Para x = 2 a função é positiva (acima do eixo x)
Em algum lugar entre 0 e 2 o gráfico da função vai cortar o eixo x ---> é a raiz

Elcioschin- Grande Mestre

- Mensagens : 73174
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: EN-1993
Re: EN-1993
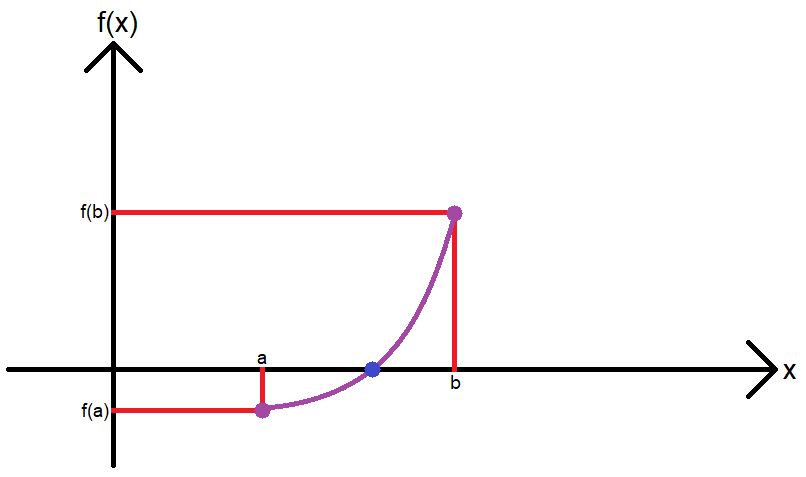
Bom, tentando explicar intuitivamente, pode-se observar que se pegarmos um ponto nos quadrantes negativos e um ponto nos quadrantes positivos, torna-se impossível criar uma linha (que no caso é um pedaço da função) que não toque o eixo 'x'.
No caso, se a função for injetiva, então esse ponto deve ter o valor 'x' entre os valores 'a' e 'b'.
Com isso,
f(a)*f(b) < 0 ⇒ ∃f(x) = 0| x∈(a,b)
f(x) é injetiva
Messias Castro- Recebeu o sabre de luz

- Mensagens : 105
Data de inscrição : 26/02/2021
Idade : 26
Localização : Fortaleza, CE
eumilenalmeida gosta desta mensagem
 Re: EN-1993
Re: EN-1993
Ficou bem claro agora! incrivel como em algumas questões da EN a resolução mais "simples" é a intuitiva. Obrigada pelo esclarecimento!

eumilenalmeida- Iniciante
- Mensagens : 9
Data de inscrição : 14/02/2021
Idade : 22
Localização : São Pedro da Aldeia - RJ
natanlopes_17 gosta desta mensagem
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos