Raízes de um polinômio

por Guilhermegch Ter 20 Abr 2021, 20:22

Pessoal, boa tarde. A minha dúvida é com a seguinte questão:

Dê o conjunto solução da equação [latex]x^4+x^3-x^2=4[/latex]

Fiz por tentativa, e descobri uma raiz [latex]x=-2[/latex], mas aplicando Briot-Ruffini, temos chego em [latex]x^3-x^2+x-2=0[/latex] e não tenho como prosseguir. Joguei no gráfico e em uma calculadora e vi que tem raízes fracionárias e duas complexas igualmente fracionárias. Existe forma de continuar?

por ruanramos Ter 20 Abr 2021, 20:33

X = 2 não é raiz desta equação, pesquisando raízes encontramos x=-2 como raiz, tente com este valor.

Verá que a equação que você encontrou está errada, e para prosseguir pode pesquisar novamente a raiz da equação de 3 grau, enfim chegará a uma de 2 grau e acredito que consiga seguir dai.

por Guilhermegch Ter 20 Abr 2021, 21:00

Perdão, escrevi errado, vou até editar. Eu achei x = -2 e deu essa equação ali mesmo. Obrigado por avisar do erro.

por ruanramos Ter 20 Abr 2021, 22:43

Boa noite, realmente essa questão esta complicada de prosseguir, não vejo como achar esta outra raiz real fracionaria, nem por Girard esta saindo. Se alguém puder dar uma ajuda, irei pensar mais, por agora não me vem nada.

por ruanramos Qua 21 Abr 2021, 10:30

Bom dia colega, está questão me deixou muito intrigado, como disse iria pensar mais, infelizmente não vi saídas, joguei a formula em um site que resolve equações, absurdo!! De onde você tirou esta questão? (se me permite perguntar), está num nível bem elevado.

Irei postar a resposta da equação de 3°grau pois a resolução ficaria muito trabalhosa.

[latex]x=\frac{1}{3}\left ( 1-2\sqrt[3]{\frac{2}{47+3\sqrt{249}}}+\sqrt[3]{\frac{1}{2}(47+3\sqrt{249})} \right )[/latex]

[latex]x=\frac{1}{3}+\frac{1}{3}(1+/- i\sqrt{3})\sqrt[3]{\frac{2}{47+3\sqrt{249}}}-\frac{1}{6}(1-/+i\sqrt{3})\sqrt[3]{\frac{1}{2}(47+3\sqrt{249})}[/latex]

por Guilhermegch Qua 21 Abr 2021, 16:57

Foi de uma prova de um amigo meu (de ensino médio!!), imagino que o professor tenha cometido algum erro sem perceber. Eu fiquei a tarde toda ontem tentando pensar em alguma coisa, pensei que fosse erro meu ou algo do tipo.

Também achei um absurdo enquanto tentei fazer e começou a ir pra caminhos de termos irracionais.

Muito, muito obrigado pela ajuda =)

por orunss Sáb 24 Abr 2021, 11:34

Só colocando uma maneira diferente de ver a questão:
Isola o x³
$Raízes de um polinômio Gif$ (I)
agora usa
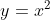$Raízes de um polinômio Gif$ em:
$Raízes de um polinômio Gif$ queremos fatorar A EXPRESSÃO do lado esquerdo da equação (I)
$Raízes de um polinômio Gif$
$Raízes de um polinômio Gif$
$Raízes de um polinômio Gif$
$Raízes de um polinômio Gif$

A partir daqui eu não sei, mas deve ter um jeito

por **Giovana Martins** Sáb 24 Abr 2021, 13:08

Acredito que este possa ser um caminho. Digo "acredito" porque, honestamente, eu não cheguei a finalizar os cálculos.

Sendo x=-2 uma das raízes, podemos reescrever p(x)=x⁴+x³-x²-4 como p(x)=(x+2)(x³-x²+x-2).

[latex]\\\mathrm{Seja\ x=u+\frac{1}{3}\ a\ transformada\ aditiva:}\\\\\mathrm{\left ( u+\frac{1}{3} \right )^3-\left ( u+\frac{1}{3} \right )^2+u-\frac{5}{3}=0\to u^3+\frac{2}{3}u-\frac{47}{27}=0}\\\\\mathrm{Por\ Cardano-Tartaglia:\ u^3+pu+q=0}\\\\\mathrm{u=\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}+\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}}\\\\\mathrm{Por\ fim,\ voltar\ em\ x=u+\frac{1}{3}.}[/latex]

Nota: a transformada aditiva foi feita para que fosse viável usar Cardano-Tartaglia, que é ideal para equações do tipo u³+pu+q=0 quando a solução desse tipo de questão não é óbvia.

por **Elcioschin** Sáb 24 Abr 2021, 14:10

Giovana voltou "com a corda toda", sempre com excelentes soluções!

Como está a faculdade?

por **Giovana Martins** Dom 25 Abr 2021, 02:36

Muito obrigada, Élcio.

Olha, com essa pandemia as coisas tem sido bem diferentes por conta do EAD, mas até aqui felizmente tudo tem caminhado bem. Devagar a gente chega lá cheers