Função Modular - Gráfico
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Função Modular - Gráfico
Função Modular - Gráfico
Boa noite.
Gostaria, por favor, de ajuda para entender como fazer o gráfico de 2 funções modulares.
Sei fazer os gráficos, por exemplo, das funções f(x) = |5x - 3|, f(x) = |x| + 1 e f(x) = |x^2 - 6x + 5|.
Mas não entendi como fazer das seguintes funções:
a) f(x) = |x|^2 - 6|x| + 5 (substitui o |x| por y e no final encontrei 4 raízes, mas não soube continuar)
b) f(x) = |2x - 3| + |x + 2|
Desde já agradeço.
Gostaria, por favor, de ajuda para entender como fazer o gráfico de 2 funções modulares.
Sei fazer os gráficos, por exemplo, das funções f(x) = |5x - 3|, f(x) = |x| + 1 e f(x) = |x^2 - 6x + 5|.
Mas não entendi como fazer das seguintes funções:
a) f(x) = |x|^2 - 6|x| + 5 (substitui o |x| por y e no final encontrei 4 raízes, mas não soube continuar)
b) f(x) = |2x - 3| + |x + 2|
Desde já agradeço.
Lana Brasil- Recebeu o sabre de luz

- Mensagens : 114
Data de inscrição : 07/04/2013
Idade : 20
Localização : sao paulo
 Re: Função Modular - Gráfico
Re: Função Modular - Gráfico
b) Invertendo a ordem ---> f(x) = |x + 2| + |2.x - 3| ---> raízes dos módulos: x = -2 e x = 3/2
Para x < - 2 ---> f(x) = - (x + 2) - (2.x - 3) ---> f(x) = - 3.x + 1
Para - 2 < x < 3/2 --> f(x) = + (x + 2) - (2.x - 3) --> f(x) = - x + 5
Para x > 3/2 ---> f(x) = + (x + 2) + (2.x - 3) ---> f(x) = 3.x - 1
Desenhe as retas em cada intervalo: para x = -2 e x = 3/2 elas terão "bolinha branca"
Para x < - 2 ---> f(x) = - (x + 2) - (2.x - 3) ---> f(x) = - 3.x + 1
Para - 2 < x < 3/2 --> f(x) = + (x + 2) - (2.x - 3) --> f(x) = - x + 5
Para x > 3/2 ---> f(x) = + (x + 2) + (2.x - 3) ---> f(x) = 3.x - 1
Desenhe as retas em cada intervalo: para x = -2 e x = 3/2 elas terão "bolinha branca"
Última edição por Elcioschin em Seg 19 Abr 2021, 19:20, editado 1 vez(es)

Elcioschin- Grande Mestre

- Mensagens : 73176
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Lana Brasil gosta desta mensagem
 Re: Função Modular - Gráfico
Re: Função Modular - Gráfico
a)
se x ≥ 0 ---> |x| = +x
se x < 0 ---> |x| = -x
portanto |x|² é sempre ≥ 0
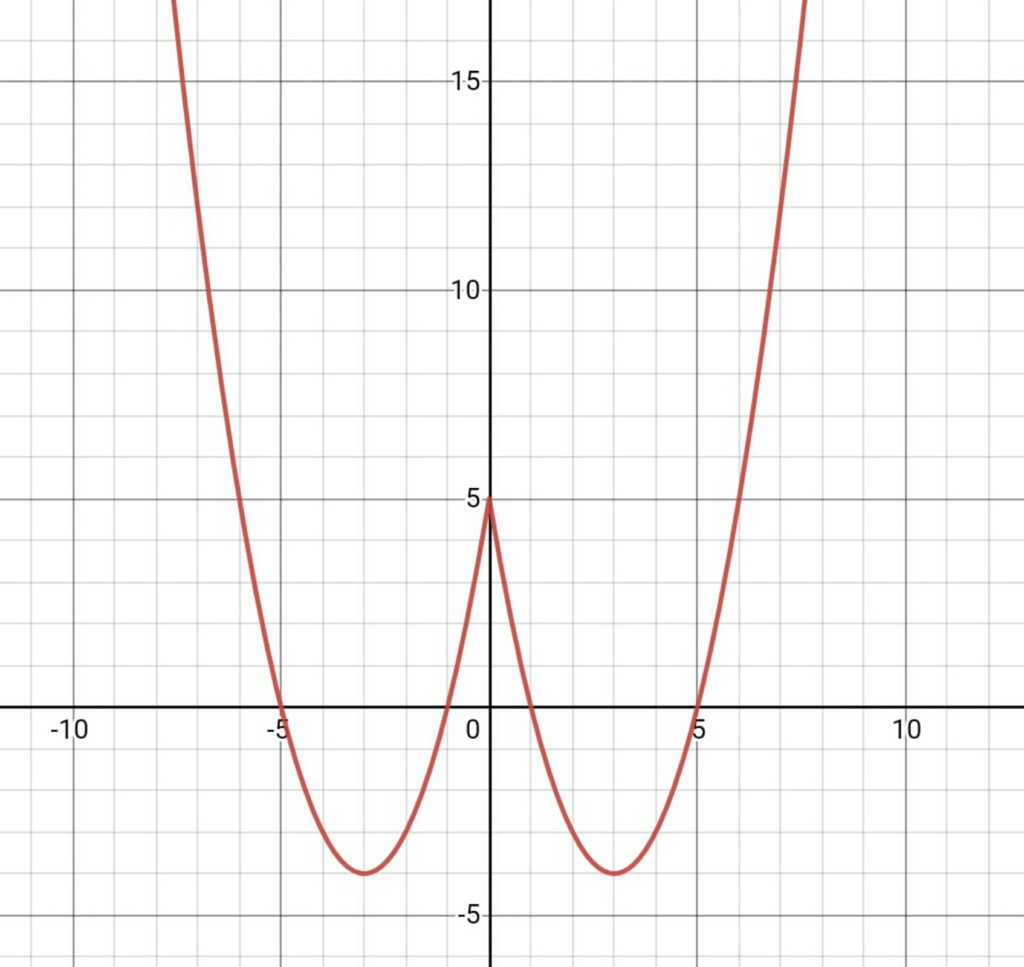
para x ≥ 0 ----> f(x) = x² - 6x + 5 ---> raízes x = 1 e x = 5 ---> vértice = (3, -4)
para x < 0 ----> f(x) = x² + 6x + 5 ---> raízes x = -1 e x = -5 ---> vértice = (-3, -4)
são duas parábolas ambas com concavidade para cima. Em ambas, para x = 0, y = 5. Note que elas têm domínios coplementares, assim f(x) é contínua em todo R.
se x ≥ 0 ---> |x| = +x
se x < 0 ---> |x| = -x
portanto |x|² é sempre ≥ 0
para x ≥ 0 ----> f(x) = x² - 6x + 5 ---> raízes x = 1 e x = 5 ---> vértice = (3, -4)
para x < 0 ----> f(x) = x² + 6x + 5 ---> raízes x = -1 e x = -5 ---> vértice = (-3, -4)
são duas parábolas ambas com concavidade para cima. Em ambas, para x = 0, y = 5. Note que elas têm domínios coplementares, assim f(x) é contínua em todo R.


Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Lana Brasil gosta desta mensagem
 Re: Função Modular - Gráfico
Re: Função Modular - Gráfico
Muito Obrigada pela ajuda!
Lana Brasil- Recebeu o sabre de luz

- Mensagens : 114
Data de inscrição : 07/04/2013
Idade : 20
Localização : sao paulo
 Tópicos semelhantes
Tópicos semelhantes» Gráfico de função modular
» Gráfico Função Modular ...
» Gráfico função modular
» Gráfico da Função Modular
» Gráfico de Função Modular
» Gráfico Função Modular ...
» Gráfico função modular
» Gráfico da Função Modular
» Gráfico de Função Modular
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












