Soma dos algarismos do apartamento
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Soma dos algarismos do apartamento
Soma dos algarismos do apartamento
No edifício mais alto da cidade moram Antônio e Eduardo.O número do andar do apartamento de Antônio coincide com o número do apartamento de Eduardo.A soma dos números dos apartamentos dos dois é  .Sabendo que há
.Sabendo que há 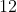 apartamentos por andar,numerados consecutivamente do primeiro andar ao último, a soma dos algarismos do apartamento de Antônio é igual a:
apartamentos por andar,numerados consecutivamente do primeiro andar ao último, a soma dos algarismos do apartamento de Antônio é igual a:
)
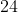
)
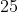
)
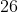
)
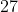
)
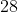
- Spoiler:
- Gabarito: (C).

Marcos- Jedi

- Mensagens : 271
Data de inscrição : 03/04/2010
Idade : 42
Localização : Rio de Janeiro
 Re: Soma dos algarismos do apartamento
Re: Soma dos algarismos do apartamento
O número do apartamento de Antônio pode ser escrito como a seguinte expressão:
_____________________________
)
• Perceba que a é o andar do apartamento
• E que, o termo -12 serve para permitir a adição de n. Assim, poderemos "escolher" o número do apartamento de determinado andar.
Ex: 2ºAndar, 12.2+n-12 = 12+n, se n for 2, temos o apartamento 14.
Note que se não houvesse o -12, avançaríamos 1 andar, então teríamos o 3ºAndar e não o 2º.
_____________________________
Podemos ver que,

_____________________________
Sabemos também, que a é o número do apartamento de Eduardo, e temos a seguinte equação:
+(a)=2164)
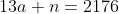
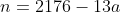
______________________________
Substituindo n na relação , podemos encontrar o valor de a:
, podemos encontrar o valor de a:




\leq -a\leq \(-166,4...))
\geq a\geq (166,4...))
Como a E N (a pertence aos Naturais)

________________________________
Agora precisamos encontrar o valor de n:

)

________________________________
E por fim, voltamos na expressão do número do apartamento de Antônio, substituindo os dados obtidos.
)
+(5-12))

___________________________________

_____________________________
• Perceba que a é o andar do apartamento
• E que, o termo -12 serve para permitir a adição de n. Assim, poderemos "escolher" o número do apartamento de determinado andar.
Ex: 2ºAndar, 12.2+n-12 = 12+n, se n for 2, temos o apartamento 14.
Note que se não houvesse o -12, avançaríamos 1 andar, então teríamos o 3ºAndar e não o 2º.
_____________________________
Podemos ver que,
_____________________________
Sabemos também, que a é o número do apartamento de Eduardo, e temos a seguinte equação:
______________________________
Substituindo n na relação
Como a E N (a pertence aos Naturais)
________________________________
Agora precisamos encontrar o valor de n:
________________________________
E por fim, voltamos na expressão do número do apartamento de Antônio, substituindo os dados obtidos.
___________________________________
 Re: Soma dos algarismos do apartamento
Re: Soma dos algarismos do apartamento
Hola.
Olimpíada De Matemática do Rio Grande do Norte.
Seja x o andar do AP de Eduardo. Então o número de seu AP é 12*(x - 1) + y, ou
1 ≤ y ≤ 12, daí:
x + 12*(x - 1) + y = 2164
x + 12x - 12 + y = 2164
13x + y = 2164 + 12
13x = 2176 - y
x = (2176 - y)/13, note que y = {1, ,2 ,3 ,4 5............}, por tentativas para que a divisão dê exata, encontramos:
quando y = 5, temos:
x = (2176 - y)/13
x = (2176 - 5)/13
x = 2171/13
x = 167
Portanto, o número do Ap de Eduardo é:
Substituindo em: 12*(x - 1) + y
12*(167 - 1) + 5
12*166 + 5
1997, logo a soma dos seus algarismos é: 1 + 9 + 9 + 7 = 26
Olimpíada De Matemática do Rio Grande do Norte.
Seja x o andar do AP de Eduardo. Então o número de seu AP é 12*(x - 1) + y, ou
1 ≤ y ≤ 12, daí:
x + 12*(x - 1) + y = 2164
x + 12x - 12 + y = 2164
13x + y = 2164 + 12
13x = 2176 - y
x = (2176 - y)/13, note que y = {1, ,2 ,3 ,4 5............}, por tentativas para que a divisão dê exata, encontramos:
quando y = 5, temos:
x = (2176 - y)/13
x = (2176 - 5)/13
x = 2171/13
x = 167
Portanto, o número do Ap de Eduardo é:
Substituindo em: 12*(x - 1) + y
12*(167 - 1) + 5
12*166 + 5
1997, logo a soma dos seus algarismos é: 1 + 9 + 9 + 7 = 26

Paulo Testoni- Membro de Honra

- Mensagens : 3409
Data de inscrição : 19/07/2009
Idade : 77
Localização : Blumenau - Santa Catarina
 Tópicos semelhantes
Tópicos semelhantes» Soma dos algarismos
» soma dos algarismos de x
» A soma dos algarismos
» [Soma dos Algarismos]
» Soma de algarismos
» soma dos algarismos de x
» A soma dos algarismos
» [Soma dos Algarismos]
» Soma de algarismos
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













