Algebra Lin.
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Algebra Lin.
por Omagodasexatas3,14 Sex 19 Mar 2021, 16:54
Seja: V espaço vetorial sobre os reais, Z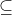 
V e x,y ∈ V. Prove que, se y ∈ [Z,x] , mas y 
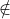[Z] , então x ∈ [Z,y], mas x 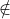[Z]. (Aqui, [Z,x] significa o subespaço gerado por Z 
{x}).
Omagodasexatas3,14- Recebeu o sabre de luz
- Mensagens : 111
Data de inscrição : 07/09/2017
Idade : 28
Localização : São Paulo, São paulo, Brasil
Re: Algebra Lin.
por SilverBladeII Seg 22 Mar 2021, 21:12
Como [latex]y \in [Z, x][/latex], existem [latex]z\in Z[/latex] e reais [latex]a, b[/latex] real tq [latex]y=az+bx[/latex]. Ora, se [latex]x \in [Z][/latex], então [latex]az+bx \in [Z][/latex] (pois é combinação linear de elementos de [latex]Z[/latex]), de modo que [latex]y\in [Z][/latex]. Pela contrapositiva, se [latex]y\not\in [Z][/latex], então [latex]x\not\in [Z][/latex].
Claro que [latex]b\neq 0[/latex], pois [latex]0x=0 \in [Z][/latex], então [latex]x=(1/b)y+(-a/b)z[/latex], uma combinação linear de elemento de [latex]Z[/latex] e [latex]y[/latex], portanto [latex]x\in[Z, y].[/latex]
Claro que [latex]b\neq 0[/latex], pois [latex]0x=0 \in [Z][/latex], então [latex]x=(1/b)y+(-a/b)z[/latex], uma combinação linear de elemento de [latex]Z[/latex] e [latex]y[/latex], portanto [latex]x\in[Z, y].[/latex]
SilverBladeII- Matador
- Mensagens : 454
Data de inscrição : 04/09/2019
Idade : 22
Localização : Teresina, Piauí, Brasil
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
