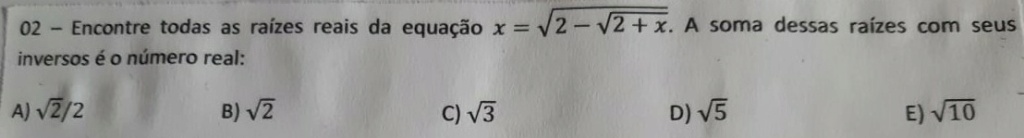Raízes da função
5 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Raízes da função
Raízes da função
Encontre todas as raízes da equação x = [2 - (2 + x)^0,5]^0,5. A Soma dessas raízes com seus inversos é o número real:
a) (2^0,5)/2
b) 2^0,5
c) 3^0,5
d) 5^0,5
e) 10^0,5
a) (2^0,5)/2
b) 2^0,5
c) 3^0,5
d) 5^0,5
e) 10^0,5
Cristina Lins- Jedi

- Mensagens : 470
Data de inscrição : 01/03/2012
Idade : 66
Localização : Itapetininga - SP
Giovana Martins e Leonardo Mariano gostam desta mensagem
 Re: Raízes da função
Re: Raízes da função
x = [2 - (2 + x)0,5]0,5 ---> x² = 2 - (2 + x)0,5 ---> (2 + x)0,5 = 2 - x²
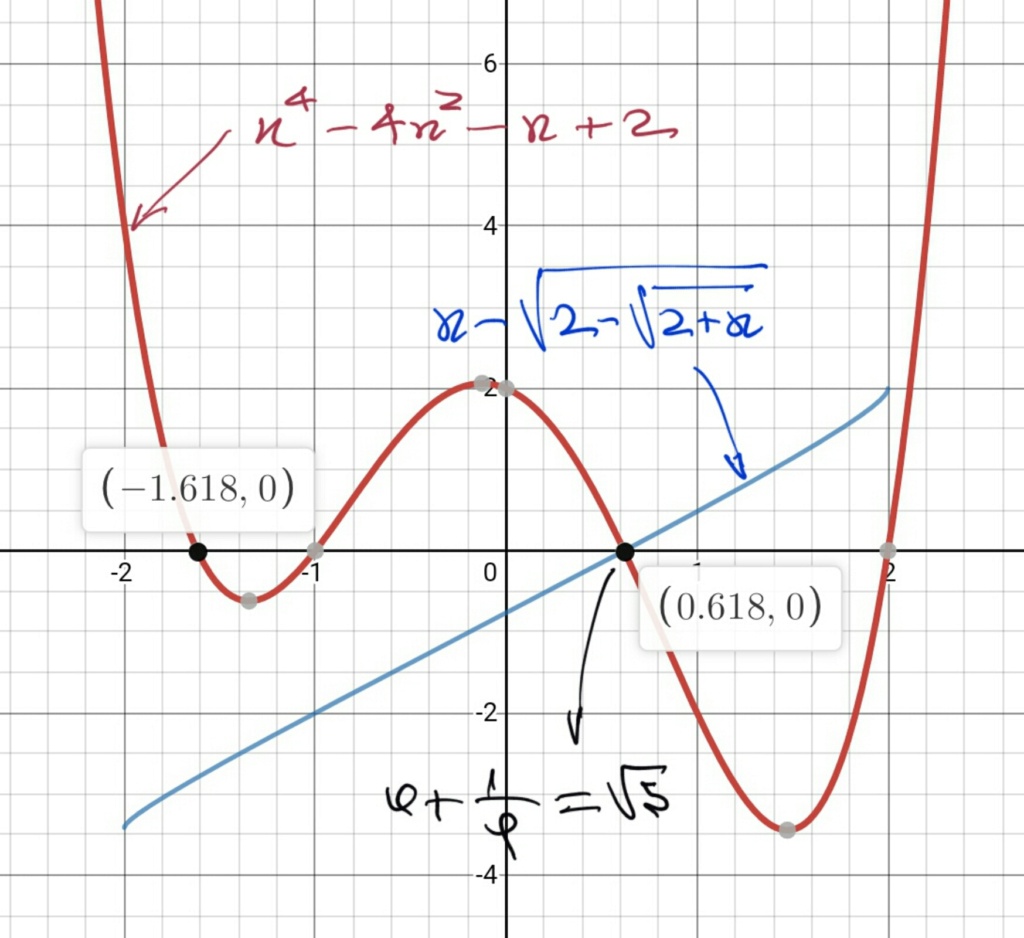
2 + x = (2 - x²)² ---> x4- 4.x² - x + 2 = 0
Teorema das raízes racionais:
As possíveis raízes racionais, se existirem, são -2, -1, 1, 2
Testando com Briott- Ruffini, vê-se que x = -1 e x = 2 são raízes:
__|1 0. -4 -1 2
-1|1 -1 -3 .2. 0
.2|1 .1. -1 0
O quociente da divisão restante x² + x - 1 = 0 ---> As duas outras raízes são:
x = (-1 + √5)/2 e x = (-1 - √5)/2
Soma das raízes: S' = - 1 + 2 + (-1 + √5)/2 + (-1 - √5)/2 ---> S' = 0
Soma dos inversos das raízes: S" = - 1 + 1/2 + 2/(-1 + √5) + 2/(-1 - √5)
Calcule S" e depois S = S' + S"
2 + x = (2 - x²)² ---> x4- 4.x² - x + 2 = 0
Teorema das raízes racionais:
As possíveis raízes racionais, se existirem, são -2, -1, 1, 2
Testando com Briott- Ruffini, vê-se que x = -1 e x = 2 são raízes:
__|1 0. -4 -1 2
-1|1 -1 -3 .2. 0
.2|1 .1. -1 0
O quociente da divisão restante x² + x - 1 = 0 ---> As duas outras raízes são:
x = (-1 + √5)/2 e x = (-1 - √5)/2
Soma das raízes: S' = - 1 + 2 + (-1 + √5)/2 + (-1 - √5)/2 ---> S' = 0
Soma dos inversos das raízes: S" = - 1 + 1/2 + 2/(-1 + √5) + 2/(-1 - √5)
Calcule S" e depois S = S' + S"
Última edição por Elcioschin em Sáb 02 Jan 2021, 09:59, editado 4 vez(es)

Elcioschin- Grande Mestre

- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Giovana Martins e Leonardo Mariano gostam desta mensagem
Cristina Lins- Jedi

- Mensagens : 470
Data de inscrição : 01/03/2012
Idade : 66
Localização : Itapetininga - SP
Giovana Martins e Leonardo Mariano gostam desta mensagem
 Re: Raízes da função
Re: Raízes da função
Refiz minha solução e deixei os cálculos finais para você fazer.
Confira minhas contas, por favor, e complete.
Outro modo de fazer, sem calcular as raízes de x4 + 0.x³ - 4.x² - x + 2 = 0
Sejam r, s, t, u as raízes. Pelas Relações de Girard:
r + s + t + u = 0 ---> Conferiu com S'
r.s + r.t + r.u + s.t + s.u + t.u = - 4
r.s.t + r.s.u + r.t.u + s.t.u = 1
r.s.t.u = 2
S = (r + s + t + u) + (1/r + 1/s + 1/t + 1/u)
S = (r + s + t + u) + (r.s.t + r.s.u + r.t.u + s.t.u)/r.s.t.u
Complete
Confira minhas contas, por favor, e complete.
Outro modo de fazer, sem calcular as raízes de x4 + 0.x³ - 4.x² - x + 2 = 0
Sejam r, s, t, u as raízes. Pelas Relações de Girard:
r + s + t + u = 0 ---> Conferiu com S'
r.s + r.t + r.u + s.t + s.u + t.u = - 4
r.s.t + r.s.u + r.t.u + s.t.u = 1
r.s.t.u = 2
S = (r + s + t + u) + (1/r + 1/s + 1/t + 1/u)
S = (r + s + t + u) + (r.s.t + r.s.u + r.t.u + s.t.u)/r.s.t.u
Complete

Elcioschin- Grande Mestre

- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Giovana Martins e Leonardo Mariano gostam desta mensagem
 Re: Raízes da função
Re: Raízes da função
Boa tarde
Cheguei nas suas raízes, mas S" me deu 1/2. Logo S = 1/2. não tem esta resposta.
Cheguei nas suas raízes, mas S" me deu 1/2. Logo S = 1/2. não tem esta resposta.
Cristina Lins- Jedi

- Mensagens : 470
Data de inscrição : 01/03/2012
Idade : 66
Localização : Itapetininga - SP
Leonardo Mariano gosta desta mensagem
 Re: Raízes da função
Re: Raízes da função
Eu não cheguei a fazer as contas (fiz no olhômetro), mas talvez uma outra saída seja por substituição trigonométrica. Veja
À esquerda da equação: x ≥ 0 e à direita: x + 2 ≥ 0, logo x ≥ -2. Seja θ ∈ [0,∏/2] tal que x=2cos(θ). Eu fiz um esboço aqui mas parece que eu errei alguma conta no meio do caminho. Eu pelo menos estava esperando chegar numa outra equação quando eu fiz. Por favor, verifique as contas (ao longo delas eu fui usando as propriedades do arco metade. Qualquer coisa eu volto aqui a noite, com mais tempo, para tentar resolver caso esta seja uma possível saída.
[latex]\\x=\sqrt{2-\sqrt{ 2+x }}\to 2cos(\theta )=\sqrt{2-\sqrt{2+2cos(\theta )}}\\\\ 2cos(\theta )=\sqrt{2-\sqrt{2[1+cos(\theta ) ]} }\to 2cos(\theta )=\sqrt{2-2cos\left ( \frac{\theta }{2} \right )}\\\\2cos(\theta )=\sqrt{2\left [1-cos\left ( \frac{\theta }{2} \right ) \right ]}\to 2cos(\theta )=\sqrt{4sen^2\left ( \frac{\theta }{4 } \right )}\\\\cos(\theta )=sen\left ( \frac{\theta }{4 } \right )\to sen\left ( \frac{\pi }{ 2}-\theta \right )=sen\left ( \frac{\theta }{4 } \right )[/latex]
À esquerda da equação: x ≥ 0 e à direita: x + 2 ≥ 0, logo x ≥ -2. Seja θ ∈ [0,∏/2] tal que x=2cos(θ). Eu fiz um esboço aqui mas parece que eu errei alguma conta no meio do caminho. Eu pelo menos estava esperando chegar numa outra equação quando eu fiz. Por favor, verifique as contas (ao longo delas eu fui usando as propriedades do arco metade. Qualquer coisa eu volto aqui a noite, com mais tempo, para tentar resolver caso esta seja uma possível saída.
[latex]\\x=\sqrt{2-\sqrt{ 2+x }}\to 2cos(\theta )=\sqrt{2-\sqrt{2+2cos(\theta )}}\\\\ 2cos(\theta )=\sqrt{2-\sqrt{2[1+cos(\theta ) ]} }\to 2cos(\theta )=\sqrt{2-2cos\left ( \frac{\theta }{2} \right )}\\\\2cos(\theta )=\sqrt{2\left [1-cos\left ( \frac{\theta }{2} \right ) \right ]}\to 2cos(\theta )=\sqrt{4sen^2\left ( \frac{\theta }{4 } \right )}\\\\cos(\theta )=sen\left ( \frac{\theta }{4 } \right )\to sen\left ( \frac{\pi }{ 2}-\theta \right )=sen\left ( \frac{\theta }{4 } \right )[/latex]

Giovana Martins- Grande Mestre

- Mensagens : 8544
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Leonardo Mariano gosta desta mensagem
 Re: Raízes da função
Re: Raízes da função
Eu resolvi da mesma maneira que o Mestre Elcio, mas retirando as raízes inválidas que foram inseridas quando a equação foi elevada ao quadrado:
[latex] x^4 -4x^2 -x+2 = 0 \rightarrow x = \left \{ -1, 2, \frac{-1 + \sqrt{5}}{2}, \frac{-1 - \sqrt{5}}{2} \right \} [/latex]
Verificando as raízes na equação original e também com as condições de existência, apenas [latex] \frac{-1 + \sqrt{5}}{2} [/latex] satisfaz.
Soma:
[latex] \frac{-1 + \sqrt{5}}{2} + \frac{1}{\frac{-1 + \sqrt{5}}{2}} \rightarrow \frac{-1 + \sqrt{5}}{2} + \frac{2}{-1 + \sqrt{5}} . \frac{1 + \sqrt{5}}{1 + \sqrt{5}} \rightarrow \\ \frac{-1 + \sqrt{5}}{2} + \frac{2(1 + \sqrt{5})}{5 - 1} \rightarrow \frac{-1 + \sqrt{5}}{2} + \frac{1 + \sqrt{5}}{2} \rightarrow \\ \frac{2 \sqrt{5}}{2} \rightarrow \sqrt{5} [/latex]
[latex] x^4 -4x^2 -x+2 = 0 \rightarrow x = \left \{ -1, 2, \frac{-1 + \sqrt{5}}{2}, \frac{-1 - \sqrt{5}}{2} \right \} [/latex]
Verificando as raízes na equação original e também com as condições de existência, apenas [latex] \frac{-1 + \sqrt{5}}{2} [/latex] satisfaz.
Soma:
[latex] \frac{-1 + \sqrt{5}}{2} + \frac{1}{\frac{-1 + \sqrt{5}}{2}} \rightarrow \frac{-1 + \sqrt{5}}{2} + \frac{2}{-1 + \sqrt{5}} . \frac{1 + \sqrt{5}}{1 + \sqrt{5}} \rightarrow \\ \frac{-1 + \sqrt{5}}{2} + \frac{2(1 + \sqrt{5})}{5 - 1} \rightarrow \frac{-1 + \sqrt{5}}{2} + \frac{1 + \sqrt{5}}{2} \rightarrow \\ \frac{2 \sqrt{5}}{2} \rightarrow \sqrt{5} [/latex]

Leonardo Mariano- Monitor

- Mensagens : 647
Data de inscrição : 11/11/2018
Idade : 22
Localização : Criciúma/SC
Medeiros e Giovana Martins gostam desta mensagem

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Giovana Martins e Leonardo Mariano gostam desta mensagem

Giovana Martins- Grande Mestre

- Mensagens : 8544
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Leonardo Mariano gosta desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» Raizes de Função
» Raízes de uma função
» Função Quadrática (Raízes)
» Função Segundo Grau Com Raizes
» Soma das raízes da função
» Raízes de uma função
» Função Quadrática (Raízes)
» Função Segundo Grau Com Raizes
» Soma das raízes da função
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos