Matriz e produto escalar.
2 participantes
Página 1 de 1
 Matriz e produto escalar.
Matriz e produto escalar.
Seja B=  e
e  .
.
Se o número real é o produto escalar dos vetores
é o produto escalar dos vetores  e
e  , então o valor de
, então o valor de  , onde
, onde  é o ângulo formado entre
é o ângulo formado entre 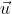 e
e 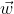 vale:
vale:





Se o número real

Eduardo Rabelo- Fera

- Mensagens : 638
Data de inscrição : 23/06/2020
Idade : 20
Localização : Curitiba
 Re: Matriz e produto escalar.
Re: Matriz e produto escalar.
Olá Eduardo! 
Não consegui encontrar nenhuma das alternativas, e não sei se estou errando algo ou se há algo errado na questão. De qualquer forma, deixarei aqui a minha solução:
Primeiro, vamos calcular o D:
[latex]\\\bullet\; B^2=\begin{bmatrix}1 & 2 & 0\\ 3& -4 &5 \\ 0& -1 &2 \end{bmatrix}\cdot\begin{bmatrix}1 & 2 & 0\\ 3& -4 &5 \\ 0& -1 &2 \end{bmatrix}=\begin{bmatrix}7 & -6 & 10\\ -9& 17 &-10\\ -3& 2 &-1 \end{bmatrix}\\\\ \rightarrow\;D=B^2-4B+3I\\\\ =\begin{bmatrix}7 & -6 & 10\\ -9& 17 &-10\\ -3& 2 &-1 \end{bmatrix} -\begin{bmatrix}4 & 8 & 0\\ 12& -16 &20 \\ 0& -4 &8\end{bmatrix} +\begin{bmatrix}3 & 0 & 0\\0& 3 &0\\0&0 &3 \end{bmatrix}\\\\ =\begin{bmatrix}6 & -14 & 10\\ -21& 36 &-30\\ -3& 6 &-6 \end{bmatrix}[/latex]
Com isso, a soma N dos elementos da diagonal principal D é 36. Agora, vamos calcular a constante 'a':
[latex]\\N=\vec{u}\cdot\vec{w}\rightarrow36=10+11a+4\rightarrow a=2[/latex]
Portanto, u = (2,11,1) e w = (5,2,4). Utilizando a fórmula do produto escalar para encontrar o cosseno de θ:
[latex]\\\cos\theta=\frac{\vec{u}\cdot\vec{w}}{|\vec{u}|.|\vec{w}|}=\frac{36}{9\sqrt{70}}=\frac{4}{\sqrt{70}}\\\\ \rightarrow\tan^2\theta=\frac{1}{\cos^2\theta}-1=\frac{70}{16}-1 =\frac{54}{16}\\\\ \rightarrow \boxed{\tan\theta = \frac{3\sqrt{6}}{4}}[/latex]
Não consegui encontrar nenhuma das alternativas, e não sei se estou errando algo ou se há algo errado na questão. De qualquer forma, deixarei aqui a minha solução:
Primeiro, vamos calcular o D:
[latex]\\\bullet\; B^2=\begin{bmatrix}1 & 2 & 0\\ 3& -4 &5 \\ 0& -1 &2 \end{bmatrix}\cdot\begin{bmatrix}1 & 2 & 0\\ 3& -4 &5 \\ 0& -1 &2 \end{bmatrix}=\begin{bmatrix}7 & -6 & 10\\ -9& 17 &-10\\ -3& 2 &-1 \end{bmatrix}\\\\ \rightarrow\;D=B^2-4B+3I\\\\ =\begin{bmatrix}7 & -6 & 10\\ -9& 17 &-10\\ -3& 2 &-1 \end{bmatrix} -\begin{bmatrix}4 & 8 & 0\\ 12& -16 &20 \\ 0& -4 &8\end{bmatrix} +\begin{bmatrix}3 & 0 & 0\\0& 3 &0\\0&0 &3 \end{bmatrix}\\\\ =\begin{bmatrix}6 & -14 & 10\\ -21& 36 &-30\\ -3& 6 &-6 \end{bmatrix}[/latex]
Com isso, a soma N dos elementos da diagonal principal D é 36. Agora, vamos calcular a constante 'a':
[latex]\\N=\vec{u}\cdot\vec{w}\rightarrow36=10+11a+4\rightarrow a=2[/latex]
Portanto, u = (2,11,1) e w = (5,2,4). Utilizando a fórmula do produto escalar para encontrar o cosseno de θ:
[latex]\\\cos\theta=\frac{\vec{u}\cdot\vec{w}}{|\vec{u}|.|\vec{w}|}=\frac{36}{9\sqrt{70}}=\frac{4}{\sqrt{70}}\\\\ \rightarrow\tan^2\theta=\frac{1}{\cos^2\theta}-1=\frac{70}{16}-1 =\frac{54}{16}\\\\ \rightarrow \boxed{\tan\theta = \frac{3\sqrt{6}}{4}}[/latex]

Victor011- Fera

- Mensagens : 663
Data de inscrição : 21/10/2015
Idade : 26
Localização : Rio de Janeiro, Brasil
 Re: Matriz e produto escalar.
Re: Matriz e produto escalar.
Victor, estava chegando nesse mesmo resultado kkkkk. Pesquisei a questão e não consegui encontrar nem o ano da prova. Talvez esse meu enunciado esteja errado. Tanto é que não faz muito sentido ser um ângulo de tangente negativa.

Eduardo Rabelo- Fera

- Mensagens : 638
Data de inscrição : 23/06/2020
Idade : 20
Localização : Curitiba
Victor011 gosta desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» PRODUTO VETORIAL, PROJEÇÃO ORTOGONAL, PRODUTO ESCALAR..
» Operações entre produto vetorial e produto escalar
» Produto Escalar
» Produto escalar e produto vetorial
» Produto Escalar
» Operações entre produto vetorial e produto escalar
» Produto Escalar
» Produto escalar e produto vetorial
» Produto Escalar
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












