Volume da pirâmide
3 participantes
Página 1 de 1
Volume da pirâmide
por jc_mamede Ter 03 Nov 2020, 11:38
Um recipiente com a forma de uma pirâmide regular, cuja base
é um quadrado de lado medindo 32 cm, contém 5820 cm^3
de areia. A altura do nível da areia nesse recipiente corresponde a 5/8
da altura total da pirâmide, conforme mostra a figura.
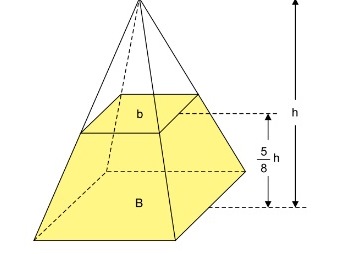
Para preencher completamente esse recipiente, será neces-
sário adicionar um volume de areia igual a
(A) 372 cm^3
(B) 300 cm^3
(C) 660 cm^3
(D) 468 cm^3
(E) 324 cm^3
GABARITO: E
é um quadrado de lado medindo 32 cm, contém 5820 cm^3
de areia. A altura do nível da areia nesse recipiente corresponde a 5/8
da altura total da pirâmide, conforme mostra a figura.
Para preencher completamente esse recipiente, será neces-
sário adicionar um volume de areia igual a
(A) 372 cm^3
(B) 300 cm^3
(C) 660 cm^3
(D) 468 cm^3
(E) 324 cm^3
GABARITO: E
Última edição por jc_mamede em Ter 03 Nov 2020, 15:27, editado 1 vez(es)
jc_mamede- Iniciante
- Mensagens : 40
Data de inscrição : 12/10/2019
Idade : 26
Localização : Manaus, Amazonas, Brasil
Re: Volume da pirâmide
por Rory Gilmore Ter 03 Nov 2020, 13:37
I) Cálculo da razão de semelhança entre as duas pirâmides:
k = (3h/
: h
k = 3/8 (razão de semelhança entre as duas pirâmides).
II) Cálculo da área b:
b/1024 = (3/²
b = 144 cm².
III) Pela diferença entre os volumes das duas pirâmides:
1024.h - b.(3h/ = 5820
1024.h - 144.3.h/8 = 5820
1024.h - 54.h = 5820
970.h = 5820
h = 6 cm.
IV) Cálculo do volume necessário (pirâmide menor):
V = 144.(3.h/
V = 144.(3.6/
V = 324 cm³.
k = (3h/
: hk = 3/8 (razão de semelhança entre as duas pirâmides).
II) Cálculo da área b:
b/1024 = (3/
²b = 144 cm².
III) Pela diferença entre os volumes das duas pirâmides:
1024.h - b.(3h/
= 58201024.h - 144.3.h/8 = 5820
1024.h - 54.h = 5820
970.h = 5820
h = 6 cm.
IV) Cálculo do volume necessário (pirâmide menor):
V = 144.(3.h/
V = 144.(3.6/
V = 324 cm³.
Rory Gilmore- Monitor
- Mensagens : 1878
Data de inscrição : 28/05/2019
Localização : Yale University - New Haven, Connecticut
jc_mamede gosta desta mensagem
Elcioschin- Grande Mestre
- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
jc_mamede gosta desta mensagem
Tópicos semelhantes» Pirâmide - Volume.
» Volume de Pirâmide
» Volume de uma pirâmide
» Volume de pirâmide
» Volume da piramide
» Volume de Pirâmide
» Volume de uma pirâmide
» Volume de pirâmide
» Volume da piramide
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
