Equação trigonomética

Resolva a equação Trigonométrica Abaixo 
U=[0;2 ∏]





[latex]4senxcosx+3^{\frac{1}{2}}=0[/latex]


GABARITO: [latex]S=(X\epsilon R/X=\frac{2\sqcap }{3};\frac{5\sqcap }{6};\frac{5\sqcap }{3};\frac{11\sqcap }{6})[/latex]

Serg.io, você pegou essa questão da onde ?

marcosprb escreveu:Serg.io, você pegou essa questão da onde ?

Aref volume 3

Serg.io escreveu:

marcosprb escreveu:Serg.io, você pegou essa questão da onde ?

Aref volume 3

Você pode me dizer qual é o número da questão ? Acho que eu tenho elas resolvida aqui no caderno.

marcosprb escreveu:

Serg.io escreveu:

marcosprb escreveu:Serg.io, você pegou essa questão da onde ?

Aref volume 3

Você pode me dizer qual é o número da questão ? Acho que eu tenho elas resolvida aqui no caderno.

Exercícios Suplementares
Questão II.38 da página 120

Salve Brow, tudo bem?

Então. Utilizando a fórmula do cosseno do arco duplo, obtemos:



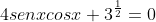
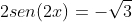
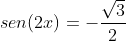------------------ ou  

E portanto, obtemos o seguinte conjunto de soluções:




Espero ter ajudado! Grande Abraço!

FocoNoITA escreveu:Salve Brow, tudo bem?

Então. Utilizando a fórmula do cosseno do arco duplo, obtemos:



------------------ ou  

E portanto, obtemos o seguinte conjunto de soluções:




Espero ter ajudado! Grande Abraço!

Olá , você acha que teria como fazer sem usar arco duplo ?

Eu estava tentando fazer assim

4senxcosx=-√3
(4senxcosx)^2=(-√3)^2
16sen^2xcos^2x=3
16cos^2x(1-cos^2x)=3
16cos^2x-16cos^4x=3
-16cos^4x+16cos^2x-3=0
Cosx=+√3/2, -√3/2 ou +1/2 , -1/2
Resolvendo essa equação daria

X = { π/6; 11π/6 ; 5π/6;7π/6;π/3;5π/3;2π/3; 4π/3}
Esses valores não correspondem ao gabarito

Será que você poderia me mostrar o que eu estou errando ? Obrigado

Perceba que inicialmente você tem que:

4senxcosx = -√3

Aqui, antes de elevar ao quadrado, você tem que analisar a equação, veja que no lado direito dela, o "-√3" é sempre negativo, então o lado esquerdo dela também tem que sempre ser negativo, ou seja, "4senxcosx" tem que sempre ser menor que zero, no caso devemos ter "4senxcosx < 0", depois de impor essa restrição, você pode elevar ao quadrado e continuar resolvendo normalmente. Essa restrição vem porque quando se eleva ao quadrado pode acabar aparecendo raízes indesejadas, veja que na sua resposta apareceu mais valores do que deveria, mas agora que você tem a restrição  "4senxcosx < 0", basta ver quais valores que você chegou que satisfazem isso, assim você vai chegar ao gabarito da questão.

Sempre que você tem uma equação que tem uma raiz de índice par, você tem que ter cuidado ao elevar a equação a esse índice por causa dessas restrições que você tem que tomar.

fantecele escreveu:Perceba que inicialmente você tem que:

4senxcosx = -√3

Aqui, antes de elevar ao quadrado, você tem que analisar a equação, veja que no lado direito dela, o "-√3" é sempre negativo, então o lado esquerdo dela também tem que sempre ser negativo, ou seja, "4senxcosx" tem que sempre ser menor que zero, no caso devemos ter "4senxcosx < 0", depois de impor essa restrição, você pode elevar ao quadrado e continuar resolvendo normalmente. Essa restrição vem porque quando se eleva ao quadrado pode acabar aparecendo raízes indesejadas, veja que na sua resposta apareceu mais valores do que deveria, mas agora que você tem a restrição  "4senxcosx < 0", basta ver quais valores que você chegou que satisfazem isso, assim você vai chegar ao gabarito da questão.

Sempre que você tem uma equação que tem uma raiz de índice par, você tem que ter cuidado ao elevar a equação a esse índice por causa dessas restrições que você tem que tomar.

Muito obrigado , essa dica me ajudou muito ! Consegui chegar ao gabarito