Triângulo Retângulo

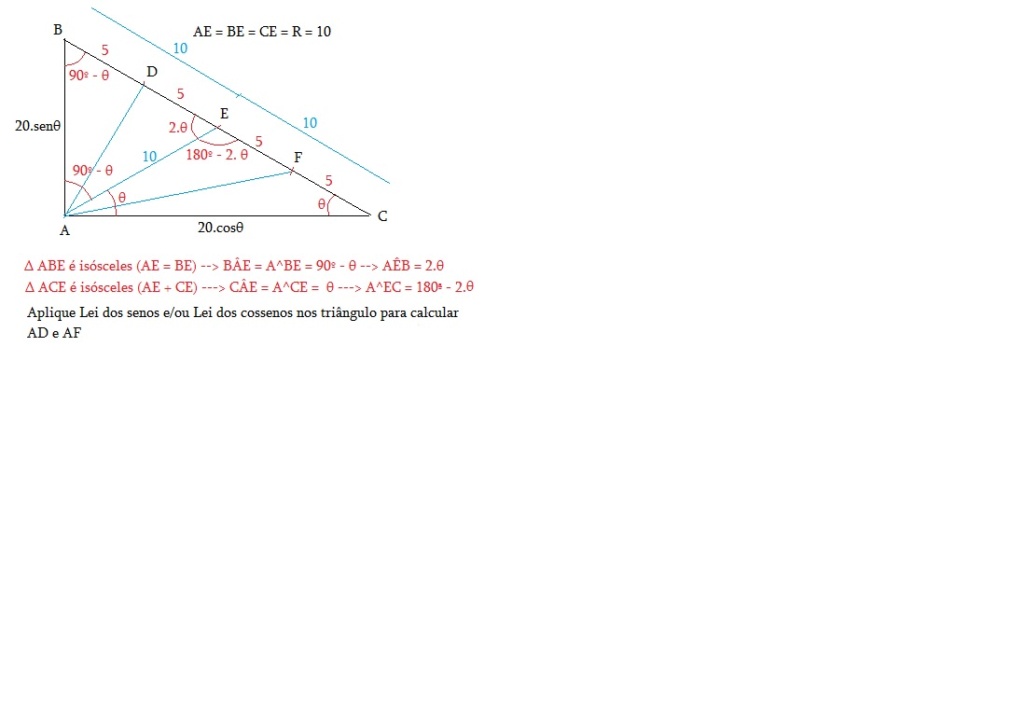
A hipotenusa [latex]\overline{BC}[/latex] de um triângulo retângulo ABC é dividida em 4 segmentos congruentes pelos pontos D, E e F. Se BC = 20, quanto vale a soma AD² + AE² + AF²?
a) 100
b) 200
c) 250
d) 350 (correta)
e) 400

Uma figura para ajudar:

Olá, ewertonaraujo22! Vamos lá:

•Inicialmente constroe-se o triângulo ABC dispondo-se os pontos D,E e F, respectivamente, na direção B para C.
•Logo, como a hipotenusa vale 20 e ela foi dividida em 4 segmentos iguais, cada um dos segmentos medirão 20÷4=5.
•Agora perceba que o segmento AE é a mediana relativa à hipotenusa e, portanto, vale a metade da hipotenuza.
•Então, nessa etapa eu apliquei a Relação de Stewart nos triângulos AEB e AEC e encontrei, respectivamente, as relações:
AD²=25+(AB²)/2
AF²=25+(AC²)/2
Agora basta resolver AE²+AF²+AD²:
100+[25+(AC²)]+ [ 25+(AB²)/2]= 150+ (AC²+AB²)/2. Agora lembre do Teorema de Pitágoras :AB²+AC²=BC²=400.
Continuando:
150+400/2=150+200=350.


Espero ter ajudado, e, se tiver dúvida, é só perguntar! Tmj

Olá ewerton  ,
fiz a questão de uma formar não convencional, e não sei se é a melhor solução. De qualquer forma, deixarei ela aqui:

Sabemos que a mediana que sai do vértice com ângulo reto em um triângulo retângulo sempre tem medida igual à metade da hipotenusa, ou seja, BE = EC = AE = 10.  Prolongando os segmentos, podemos formar um paralelogramo ADGF. Veja:


Agora vamos usar o seguinte teorema: "para um paralelogramo, vale que a soma do quadrado dos 4 lados é igual a soma do quadrado das diagonais." Veja que DF = 10 e AG = 20. sendo assim, teremos que:

2.AD² + 2.AF² = 10² + 20² = 500 → AD² + AF² = 250

Como AE = 10:

AD² + AE² + AF² = 250 + 10² = 350