areas e volumes
3 participantes
Página 1 de 1
 areas e volumes
areas e volumes
o diametro do atomo de rubidio e 4.95 angstrom. Considerando duas maneiras diferentes de colocar os atomos em uma superficie. No arranjo a, todos os atomos estao alinhados uns com o outros. O arranjo b e chamado arranjo de empacotamento denso porque os atomos situam-se nas depressoes formadas pela fileira de atomos anterior.: A) usando o arranjo a, quantos atomos de rubidio poderiam ser colocados em uma superficie quadratica de 1,0 cm de lado?B) q2uantos atomos de Rubidio poderiam ser colocados em uma superficie quadratica usando o arranjo ? Qual o fator de aumento no numero de atomos quando se muda do arranjo b para o arranjo a? Se passarmos para tres dimensoes, qual arranjo levaria uma maior densidade para o metal Rubidio?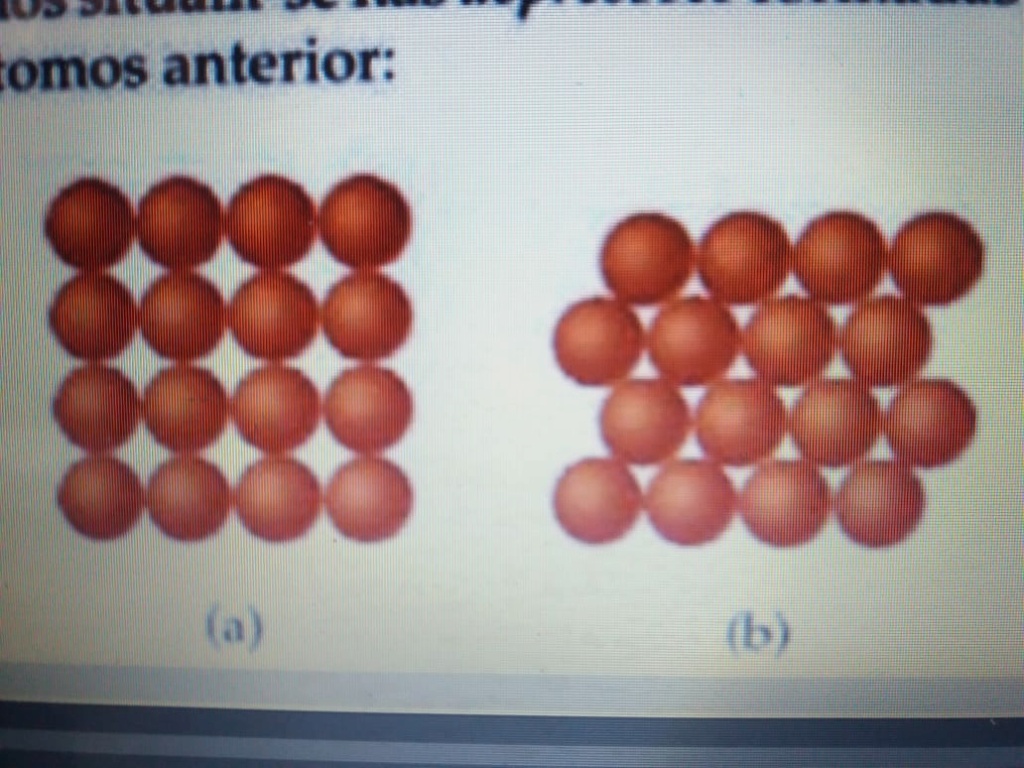


Jorge Marcelo Da Costa- Jedi

- Mensagens : 364
Data de inscrição : 01/03/2017
Idade : 44
Localização : Cascavel - Pr
 Re: areas e volumes
Re: areas e volumes
A) Sabendo que 1 Å = 10-10 m, basta realizarmos a razão entre o tamanho de cada lado da superfície e o diâmetro de cada átomo de Rubídio para sabermos quantos átomos cabem de um lado a outro da superfície:
10-2/(4,95x10-10) = 20.202.020 átomos.
Calculando a área:
20.202.020² = 408.121.612.080.400 átomos no arranjo A.
B) Imagino que a questão se refira ao arranjo B. Para, isso, calculemos a distância vertical entre o centro de um átomo de rubídio e o centro de outro átomo situado na linha logo acima. Para isso, note o triângulo retângulo de hipotenusa 2r e catetos x e r, sendo x a distância que procuramos. Por teorema de Pitágoras:
(2r)² = x² + r² -> x² = 4r² - r² = 3r² -> x = √(3r²) = r√3 Å
Isso nos permite afirmar que a cada: r + r + r√3 = 2r + r√3 = d + r√3 = 4,95 + 2,475√3 Å, verticalmente, cabem 2 átomos de rubídio. Calculemos, então, quantos desses átomos cabem ao longo do total da superfície:
2*[10-2/(4,95x10-10 + 2,475√(3)x10-10)]" = 21.652.459 átomos cabem verticalmente no arranjo B.
Horizontalmente não haverá muita variação, exceto pelo fato de que nas linhas que tiverem r Å de distância da lateral da superfície caberá menos um átomo. Nessas linhas, caberão:
20202020 - 1 = 20.202.019 átomos
Enquanto nas outras linhas caberão o número normal de 20.202.020 átomos. Esses números totalizam, portanto, 20202020 + 20202019 = 40.404.039 átomos a cada duas linhas horizontais.
Se existem 21.652.459 linhas horizontais, então existem:
21652459/2 = 10.826.229 pares dessas linhas + 0,5 = mais um par de linhas pela metade (uma linha).
10826229,5*40404039 = 437.423.398.940.950 átomos no arranjo B.
Em relação ao arranjo A, no arranjo B há um aumento no número de átomos presentes na superfície, de:
437423398940950 - 408121612080400 = 29.301.786.860.550 átomos
Logo, o fator de aumento do arranjo B para o arranjo A é de cerca de:
437423398940950/408121612080400 ≈ 1,07179 ≈ 1,07 ou, em porcentagem, ≈ 7%.
O arranjo B possuiria maior densidade se dispuséssemos ambos arranjos em três dimensões, já que para o mesmo volume caberão mais átomos dentro.
10-2/(4,95x10-10) = 20.202.020 átomos.
Calculando a área:
20.202.020² = 408.121.612.080.400 átomos no arranjo A.
B) Imagino que a questão se refira ao arranjo B. Para, isso, calculemos a distância vertical entre o centro de um átomo de rubídio e o centro de outro átomo situado na linha logo acima. Para isso, note o triângulo retângulo de hipotenusa 2r e catetos x e r, sendo x a distância que procuramos. Por teorema de Pitágoras:
(2r)² = x² + r² -> x² = 4r² - r² = 3r² -> x = √(3r²) = r√3 Å
Isso nos permite afirmar que a cada: r + r + r√3 = 2r + r√3 = d + r√3 = 4,95 + 2,475√3 Å, verticalmente, cabem 2 átomos de rubídio. Calculemos, então, quantos desses átomos cabem ao longo do total da superfície:
2*[10-2/(4,95x10-10 + 2,475√(3)x10-10)]" = 21.652.459 átomos cabem verticalmente no arranjo B.
Horizontalmente não haverá muita variação, exceto pelo fato de que nas linhas que tiverem r Å de distância da lateral da superfície caberá menos um átomo. Nessas linhas, caberão:
20202020 - 1 = 20.202.019 átomos
Enquanto nas outras linhas caberão o número normal de 20.202.020 átomos. Esses números totalizam, portanto, 20202020 + 20202019 = 40.404.039 átomos a cada duas linhas horizontais.
Se existem 21.652.459 linhas horizontais, então existem:
21652459/2 = 10.826.229 pares dessas linhas + 0,5 = mais um par de linhas pela metade (uma linha).
10826229,5*40404039 = 437.423.398.940.950 átomos no arranjo B.
Em relação ao arranjo A, no arranjo B há um aumento no número de átomos presentes na superfície, de:
437423398940950 - 408121612080400 = 29.301.786.860.550 átomos
Logo, o fator de aumento do arranjo B para o arranjo A é de cerca de:
437423398940950/408121612080400 ≈ 1,07179 ≈ 1,07 ou, em porcentagem, ≈ 7%.
O arranjo B possuiria maior densidade se dispuséssemos ambos arranjos em três dimensões, já que para o mesmo volume caberão mais átomos dentro.
Última edição por Christian M. Martins em Dom 27 Set 2020 - 15:25, editado 1 vez(es)
 Re: areas e volumes
Re: areas e volumes
ola Christian, nao entendi uma coisa: se cabem 21.652.459 átomos verticalmente no arranjo B, nao serie esse o numero de linhas verticais?

Jorge Marcelo Da Costa- Jedi

- Mensagens : 364
Data de inscrição : 01/03/2017
Idade : 44
Localização : Cascavel - Pr
 Re: areas e volumes
Re: areas e volumes
Imagine que cada átomo seja uma esfera de diâmetro 0,1 cm
Neste caso, na camada inferior caberiam 10.10 = 100 átomos
Na 2ª camada vamos colocar cada átomo no vão entre quatro átomos inferiores.
Neste caso, na 2ª camada caberiam apenas 9.9 = 81
Em compensação, na vertical os átomos ocupariam uma altura h < 0,2 cm
Na 3ª camada vamos colocar novamente 100 e na 4ª camada 81
Se continuarmos assim, a diferença de 19 átomos entre cada duas camadas sucessivas será compensada pela colocação de 1 ou mais camadas adicionais.
Neste caso, na camada inferior caberiam 10.10 = 100 átomos
Na 2ª camada vamos colocar cada átomo no vão entre quatro átomos inferiores.
Neste caso, na 2ª camada caberiam apenas 9.9 = 81
Em compensação, na vertical os átomos ocupariam uma altura h < 0,2 cm
Na 3ª camada vamos colocar novamente 100 e na 4ª camada 81
Se continuarmos assim, a diferença de 19 átomos entre cada duas camadas sucessivas será compensada pela colocação de 1 ou mais camadas adicionais.

Elcioschin- Grande Mestre

- Mensagens : 73184
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: areas e volumes
Re: areas e volumes
qual seria a conta para chegar a 23.817.705 linhas horizontais, nao entendi como chegar a esse resultado
acho que ele colocou o numero errado ali, pois continua a conta com o numero que eu acredito ser o certo:
"Isso nos permite afirmar que a cada: r + r + r√3 = 2r + r√3 = d + r√3 = 4,95 + 2,475√3 Å, verticalmente, cabem 2 átomos de rubídio. Calculemos, então, quantos desses átomos cabem ao longo do total da superfície:
2*[10-2/(4,95x10-10 + 2,475√(3)x10-10)]" = 21.652.459 átomos cabem verticalmente no arranjo B."
sendo assim ele dividiu esse total por dois e multiplicou pelo numero de atomos na horizontal
21652459/2 = 10.826.229 pares dessas linhas + 0,5 = mais um par de linhas pela metade (uma linha).
10826229,5*40404039 = 437.423.398.940.950 átomos no arranjo B.
nao entendi de onde veio 23.817.705 linhas horizontais
acho que ele colocou o numero errado ali, pois continua a conta com o numero que eu acredito ser o certo:
"Isso nos permite afirmar que a cada: r + r + r√3 = 2r + r√3 = d + r√3 = 4,95 + 2,475√3 Å, verticalmente, cabem 2 átomos de rubídio. Calculemos, então, quantos desses átomos cabem ao longo do total da superfície:
2*[10-2/(4,95x10-10 + 2,475√(3)x10-10)]" = 21.652.459 átomos cabem verticalmente no arranjo B."
sendo assim ele dividiu esse total por dois e multiplicou pelo numero de atomos na horizontal
21652459/2 = 10.826.229 pares dessas linhas + 0,5 = mais um par de linhas pela metade (uma linha).
10826229,5*40404039 = 437.423.398.940.950 átomos no arranjo B.
nao entendi de onde veio 23.817.705 linhas horizontais

Jorge Marcelo Da Costa- Jedi

- Mensagens : 364
Data de inscrição : 01/03/2017
Idade : 44
Localização : Cascavel - Pr
 Re: areas e volumes
Re: areas e volumes
Jorge Marcelo Da Costa escreveu:qual seria a conta para chegar a 23.817.705 linhas horizontais, nao entendi como chegar a esse resultado
acho que ele colocou o numero errado ali, pois continua a conta com o numero que eu acredito ser o certo:
"Isso nos permite afirmar que a cada: r + r + r√3 = 2r + r√3 = d + r√3 = 4,95 + 2,475√3 Å, verticalmente, cabem 2 átomos de rubídio. Calculemos, então, quantos desses átomos cabem ao longo do total da superfície:
2*[10-2/(4,95x10-10 + 2,475√(3)x10-10)]" = 21.652.459 átomos cabem verticalmente no arranjo B."
sendo assim ele dividiu esse total por dois e multiplicou pelo numero de atomos na horizontal
21652459/2 = 10.826.229 pares dessas linhas + 0,5 = mais um par de linhas pela metade (uma linha).
10826229,5*40404039 = 437.423.398.940.950 átomos no arranjo B.
nao entendi de onde veio 23.817.705 linhas horizontais
Já editei. Na verdade são 21.652.459 linhas horizontais, como calculado acima. Esse número de 23.817.705 linhas horizontais está errado, provavelmente digitei sem olhar para o teclado e acabei errando os números, mas pode ver que não foi ele que usei para os cálculos. Logo, apesar do erro, a resolução estava correta e continua sendo a mesma.
 Tópicos semelhantes
Tópicos semelhantes» áreas e volumes
» Áreas e volumes
» Geometria métrica e espacial. Volumes e áreas
» Geometria métrica e espacial . Volumes e áreas
» Dúvida no resultado da raiz quadrada Áreas e Volumes de Sólidos
» Áreas e volumes
» Geometria métrica e espacial. Volumes e áreas
» Geometria métrica e espacial . Volumes e áreas
» Dúvida no resultado da raiz quadrada Áreas e Volumes de Sólidos
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













