Número de Soluções Inteiras

Quantas soluções inteiras e não negativas podemos encontrar resolvendo a equação:

x+y+z+w = 5

Gabarito:
56

Fonte 1: http://br.answers.yahoo.com/question/index?qid=20070805131837AA1KIKU

Fonte 2: http://www.paulomarques.com.br/arq3-9.htm

Porque aplicando o método do paulomarques não da certo?

Ambas as fontes divergem quanto ao gabarito.

Falta de atenção minha:

x+y+z+w = 5 ---> Gabarito: 56

x+y+z=5 ---> Gabarito: 21

http://www.paulomarques.com.br/arq10-65.htm

Adam, acho que para resolver esse tipo de questão seria mais fácil usar o método do qual se deduz a fórmula do paulomarques, ao invés da fórmula em si. Vou tentar explicar aqui, usando um exemplo mais simples.

Vamos considerar primeiro a seguinte equação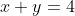 com soluções inteiras e não negativas. Para determinar o número de soluções da mesma, tendo em vista o domínio, podemos imaginar inicialmente, duas caixas, denominadas x e y e 4 bolinhas. Então as soluções serão os modos de distribuir as 4 bolas nas duas caixas, como por exemplo, 4 bolas na caixa x e nenhuma na caixa y.
Agora, troquemos a ideia de caixa por uma outra barreira espacial que permita-nos distinguir as bolas de cada caixa de forma mais simples: uma barra, ou "pauzinho". No caso, tínhamos duas caixas, que podem ser substituídas por 1 pauzinho entre as bolas. Para exemplificar, podemos distribuir as bolas(O) e o traço(/) da seguinte maneira:

OOO / O

ou então

/OOOO

Sendo o primeiro espaço pertencente a x e o segundo a y. Dessa forma, cada uma das distribuições acima, será uma solução para a equação dada. Mas como vemos, o número de distribuições dos elementos "bola" e "traço" é dado pela permutação de 5 elementos sendo 4 deles, repetidos. Tal número, no caso, é dado por , ou seja, 5, que é exatamente o número de soluções da equação.
Em suma o método é este, agora deixo contigo a extensão dele para outros casos e para uma posterior generalização. Um abraço

Esqueci de perguntar se tu já conhecia ele, mas preferiu usar a fórmula...

To aprendendo .....