Seno de 72
+2
Emanuel Dias
Lukinhas26
6 participantes
Página 1 de 1
Seno de 72
por Lukinhas26 Qua 17 Jun 2020, 14:25
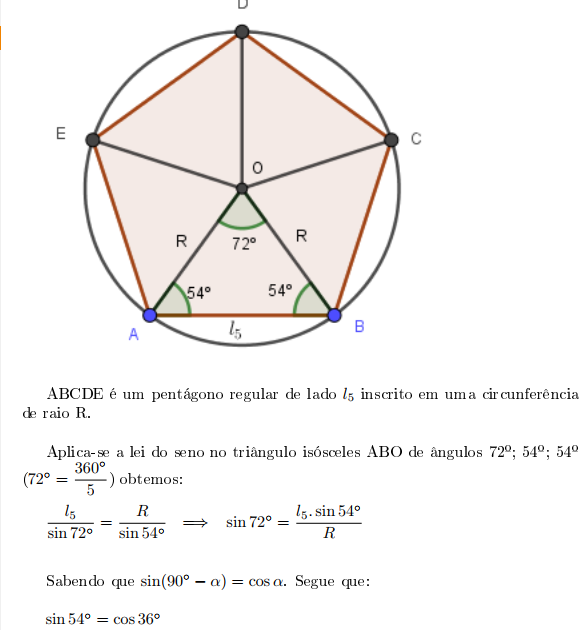
Sabe-se que o lado do pentágono regular inscrito em uma circunferência é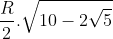 
. Sabendo disso, encontre o seno de 72.
Se puderem utilizar tão somente os aspectos da Geometria Plana para tirar minha dúvida, ficarei grato!
gabarito:
Se puderem utilizar tão somente os aspectos da Geometria Plana para tirar minha dúvida, ficarei grato!
gabarito:
Lukinhas26- Recebeu o sabre de luz
- Mensagens : 113
Data de inscrição : 07/01/2019
Idade : 42
Localização : Goiás
Re: Seno de 72
por Emanuel Dias Qua 17 Jun 2020, 14:58
Olá.
O ângulo central com extremo nos extremos de um lado mede 360º/5=72º.
Aplique lei dos senos.
O ângulo central com extremo nos extremos de um lado mede 360º/5=72º.
Aplique lei dos senos.
____________________________________________
El Álgebra no es más que Geometría y la Geometría no es más que Álgebra abstracta
Sophie Germain
Sophie Germain
Emanuel Dias- Monitor
- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
Re: Seno de 72
por Lukinhas26 Qua 17 Jun 2020, 15:14
Eu fiz isso. Muito obrigado por ajudar!
Poderia desenvolver sua conta para eu comparar com a minha?
Poderia desenvolver sua conta para eu comparar com a minha?
Lukinhas26- Recebeu o sabre de luz
- Mensagens : 113
Data de inscrição : 07/01/2019
Idade : 42
Localização : Goiás
Re: Seno de 72
por Elcioschin Qua 17 Jun 2020, 15:19
Acho que, pela Lei do senos não dá, porque não sabemos o seno de G^BC = G^CB = 54º
Seja M o ponto médio de BC. No triângulo retângulo G^MC:
B^GM = C^GM = 36º
sen(C^GM) = CM/GC ---> sen36º = (L/2)/R ---> sen36º = L/2.R --->
sen36º = [(R/2).√(10 - 2.√5)]/2.R ---> sen36º = √(10 - 2.√5)/4
Calcule cos36º
sen72º = 2.sen36º.cos36º
Seja M o ponto médio de BC. No triângulo retângulo G^MC:
B^GM = C^GM = 36º
sen(C^GM) = CM/GC ---> sen36º = (L/2)/R ---> sen36º = L/2.R --->
sen36º = [(R/2).√(10 - 2.√5)]/2.R ---> sen36º = √(10 - 2.√5)/4
Calcule cos36º
sen72º = 2.sen36º.cos36º
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Seno de 72
por Rory Gilmore Qua 17 Jun 2020, 15:36
Elcioschin, existe uma maneira. Porém é necessário fazer uma série de contas anteriores:
I) Calcula-se o apótema.
II) Calcula-se o sen de 54º.
III) Calcula-se o sen 72º pela Lei dos Senos.
I) Calcula-se o apótema.
II) Calcula-se o sen de 54º.
III) Calcula-se o sen 72º pela Lei dos Senos.
Rory Gilmore- Monitor
- Mensagens : 1878
Data de inscrição : 28/05/2019
Localização : Yale University - New Haven, Connecticut
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: Seno de 72
por Emanuel Dias Qua 17 Jun 2020, 17:51
Elcioschin escreveu:Acho que, pela Lei do senos não dá, porque não sabemos o seno de G^BC = G^CB = 54º
Seja M o ponto médio de BC. No triângulo retângulo G^MC:
B^GM = C^GM = 36º
sen(C^GM) = CM/GC ---> sen36º = (L/2)/R ---> sen36º = L/2.R --->
sen36º = [(R/2).√(10 - 2.√5)]/2.R ---> sen36º = √(10 - 2.√5)/4
Calcule cos36º
sen72º = 2.sen36º.cos36º
Verdade, não considerei que os outros ângulos não são notáveis. Ótima complementação do Rory e ótima solução do Medeiros
____________________________________________
El Álgebra no es más que Geometría y la Geometría no es más que Álgebra abstracta
Sophie Germain
Sophie Germain
Emanuel Dias- Monitor
- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
Outra solução
por tulio150 Qua 18 Ago 2021, 14:32
OUTRA SOLUÇÃO
Essa questão está no livro Fundamentos ME -9.
CAP XVI - Polígonos Regulares - Seção 2 (Cálculo de lado e apótema dos polígonos regulares)
Exercício: 724. a)
Uma forma boa de resolver é rever as demonstrações da Seção 2 e os exercícios anteriores.
Solução
Essa questão está no livro Fundamentos ME -9.
CAP XVI - Polígonos Regulares - Seção 2 (Cálculo de lado e apótema dos polígonos regulares)
Exercício: 724. a)
Uma forma boa de resolver é rever as demonstrações da Seção 2 e os exercícios anteriores.
Solução
tulio150- Iniciante
- Mensagens : 46
Data de inscrição : 21/11/2019
Idade : 45
Localização : Rio de Janeiro
Re: Seno de 72
por Medeiros Qui 19 Ago 2021, 00:19
Quando dei minha resposta, ano passado, o látex estava com falha e para mim não aparecia o valor do lado que foi dado pelo enunciado -- conforme o print screen da minha resposta. Então procurei achar o sen72° como pude.
Porém como o enunciado já fornece o valor do lado do pentágono em função de R, fica muito fácil, basta aplicar a lei dos cossenos no triângulo isósceles de lados R para achar o cos72°; depois, a relação fundamental da trigonometria.
Porém como o enunciado já fornece o valor do lado do pentágono em função de R, fica muito fácil, basta aplicar a lei dos cossenos no triângulo isósceles de lados R para achar o cos72°; depois, a relação fundamental da trigonometria.
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Tópicos semelhantes» (FUVEST)Seno e Co-seno de Arco Trigonométrico
» seno e co-seno de arco trigonométrico
» Seno de A
» Seno x+ Cos x
» SENO DE PI^2
» seno e co-seno de arco trigonométrico
» Seno de A
» Seno x+ Cos x
» SENO DE PI^2
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
