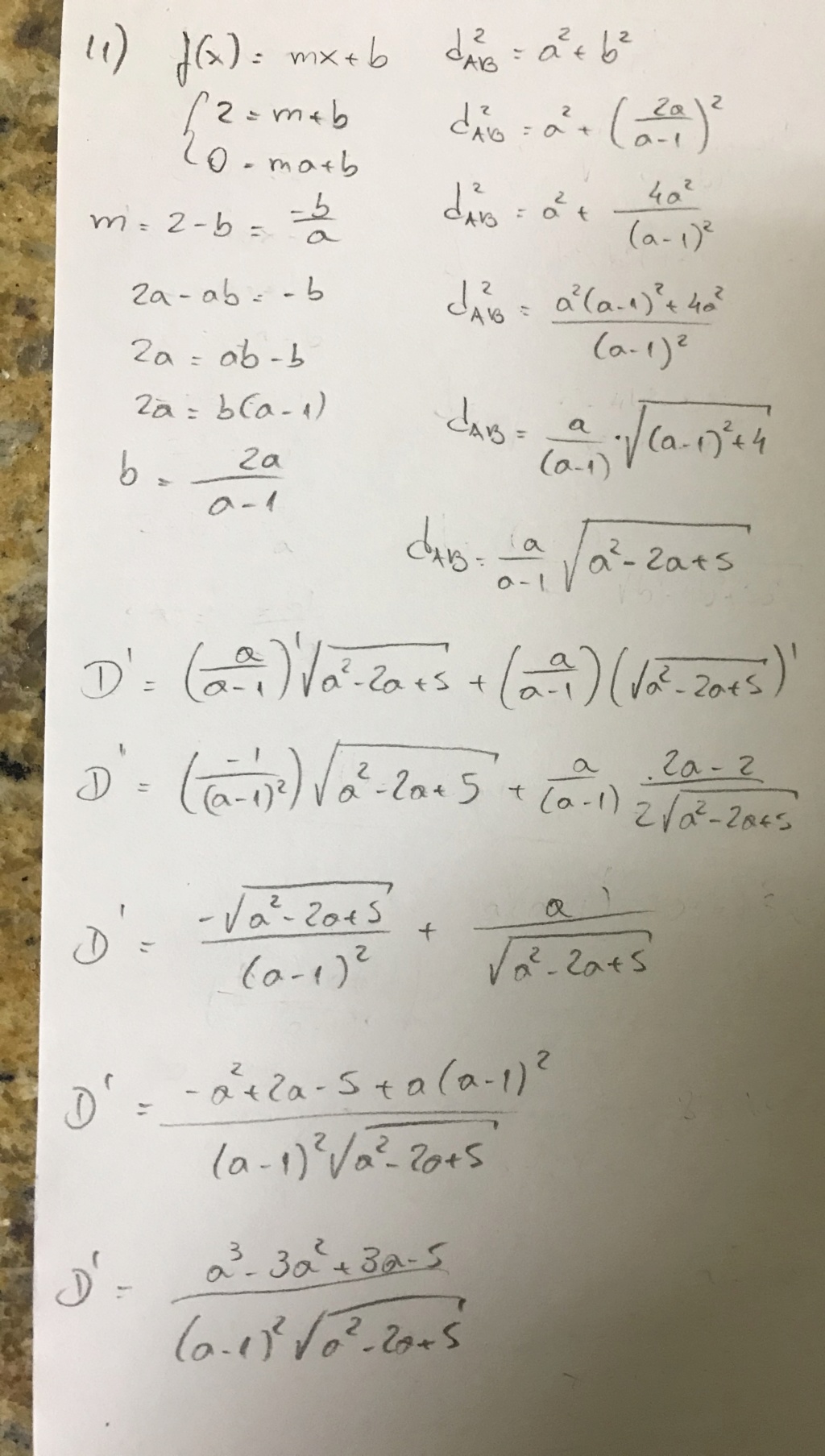maximos e minimos
2 participantes
Página 1 de 1
maximos e minimos
por rundaris Dom 24 maio 2020, 17:30
r é uma reta que passa pelo ponto (1,2) e intercepta os eixos nos pontos A = (a,0) e B = (0,b), com a > 0 e b > 0. Determine r de modo que a distancia de A a B seja a menor possivel.
Apos essa resolucao, nao consegui encontrar uma raiz para D`. Outra solucao?
Apos essa resolucao, nao consegui encontrar uma raiz para D`. Outra solucao?
Última edição por rundaris em Dom 24 maio 2020, 23:37, editado 1 vez(es)
rundaris- Padawan
- Mensagens : 64
Data de inscrição : 28/09/2013
Idade : 27
Localização : São Paulo, SP, Brasil
Re: maximos e minimos
por Elcioschin Dom 24 maio 2020, 21:56
Sua solução está correta
A equação do 3º grau tem duas raízes complexas e uma raiz real a ~= 2,6
Uma sugestão para outra solução
Na figura abaixo aparece o segmento de reta AB, pertencente à reta r
A distância d = OH da reta à origem nada mais é do que a altura do triângulo retângulo relativa à hipotenusa AB
Área de OAB = a.b/2= d.√(a² + b²)/2 ---> a².b² = d².(a² + b²)
Equação da reta r que vc já calculou: y = m.x + n --> m.x - y + n = 0
Além disso, temos a distância de um ponto O(0, 0) à reta r: y = m.x + n --> m
d = |m.0 - 1.0 + n|/(m² + n²)
Tente fazer.
A equação do 3º grau tem duas raízes complexas e uma raiz real a ~= 2,6
Uma sugestão para outra solução
Na figura abaixo aparece o segmento de reta AB, pertencente à reta r
A distância d = OH da reta à origem nada mais é do que a altura do triângulo retângulo relativa à hipotenusa AB
Área de OAB = a.b/2= d.√(a² + b²)/2 ---> a².b² = d².(a² + b²)
Equação da reta r que vc já calculou: y = m.x + n --> m.x - y + n = 0
Além disso, temos a distância de um ponto O(0, 0) à reta r: y = m.x + n --> m
d = |m.0 - 1.0 + n|/(m² + n²)
Tente fazer.
Elcioschin- Grande Mestre
- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: maximos e minimos
por rundaris Dom 24 maio 2020, 23:37
Elcioschin escreveu:Sua solução está correta
A equação do 3º grau tem duas raízes complexas e uma raiz real a ~= 2,6
Uma sugestão para outra solução
Na figura abaixo aparece o segmento de reta AB, pertencente à reta r
A distância d = OH da reta à origem nada mais é do que a altura do triângulo retângulo relativa à hipotenusa AB
Área de OAB = a.b/2= d.√(a² + b²)/2 ---> a².b² = d².(a² + b²)
Equação da reta r que vc já calculou: y = m.x + n --> m.x - y + n = 0
Além disso, temos a distância de um ponto O(0, 0) à reta r: y = m.x + n --> m
d = |m.0 - 1.0 + n|/(m² + n²)
Tente fazer.
Gostei dessa solucao, criativo. Valeu! vou tentar fazer desse jeito
rundaris- Padawan
- Mensagens : 64
Data de inscrição : 28/09/2013
Idade : 27
Localização : São Paulo, SP, Brasil
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
