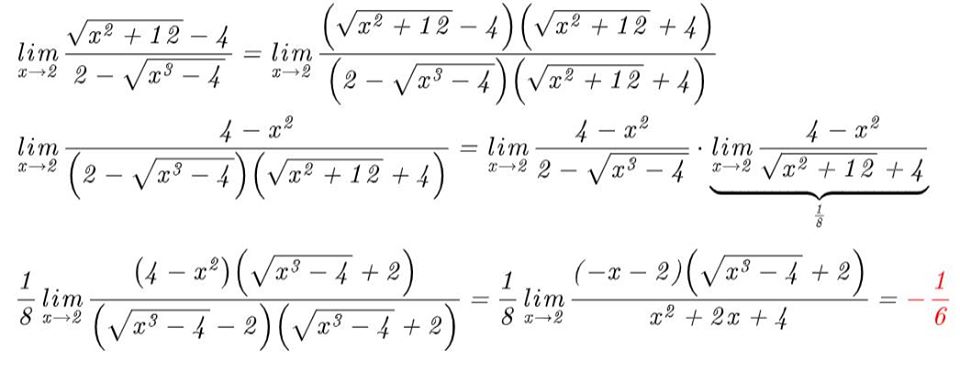limites de funções
4 participantes
Página 1 de 2
Página 1 de 2 • 1, 2 
 limites de funções
limites de funções
gostaria de resolver esses dois limites de funções sem a regra do l'hospital,mesmo sabendo que é mais fácil.
\lim_{x\rightarrow 2}=\frac{\sqrt{x^{2}+12}-4}{2-\sqrt{x^{3}-4}} \lim_{x\rightarrow \frac{1}{2}}=\frac{\sqrt[4]{2x}-1}{\sqrt{2x-1}}
\lim_{x\rightarrow 2}=\frac{\sqrt{x^{2}+12}-4}{2-\sqrt{x^{3}-4}} \lim_{x\rightarrow \frac{1}{2}}=\frac{\sqrt[4]{2x}-1}{\sqrt{2x-1}}
gabrielgosk8- Iniciante
- Mensagens : 6
Data de inscrição : 09/06/2019
Idade : 26
Localização : Osasco,São Paulo,Brasil
 Re: limites de funções
Re: limites de funções
Olá, seu latex deu problema, poderia arrumar?
____________________________________________
El Álgebra no es más que Geometría y la Geometría no es más que Álgebra abstracta
Sophie Germain
Sophie Germain
Emanuel Dias- Monitor

- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
 Re: limites de funções
Re: limites de funções
deve ser isso
\lim_{x\rightarrow 2}=\frac{\sqrt{x^{2}+12}-4}{2-\sqrt{x^{3}-4}} \lim_{x\rightarrow \frac{1}{2}}=\frac{\sqrt[4]{2x}-1}{\sqrt{2x-1}}

RavenaAaaaa- Padawan

- Mensagens : 79
Data de inscrição : 19/03/2020
 Re: limites de funções
Re: limites de funções
RavenaAaaaa escreveu:deve ser isso\lim_{x\rightarrow 2}=\frac{\sqrt{x^{2}+12}-4}{2-\sqrt{x^{3}-4}} \lim_{x\rightarrow \frac{1}{2}}=\frac{\sqrt[4]{2x}-1}{\sqrt{2x-1}}
O da direita sai fácil apenas aplicando propriedades de limites, o da esquerda ta dando mais trabalho.
____________________________________________
El Álgebra no es más que Geometría y la Geometría no es más que Álgebra abstracta
Sophie Germain
Sophie Germain
Emanuel Dias- Monitor

- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
 Re: limites de funções
Re: limites de funções
Última edição por Emanuel Dias em Seg 30 Mar 2020, 05:04, editado 1 vez(es)
____________________________________________
El Álgebra no es más que Geometría y la Geometría no es más que Álgebra abstracta
Sophie Germain
Sophie Germain
Emanuel Dias- Monitor

- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
 Re: limites de funções
Re: limites de funções
Um outro jeito por Séries de Taylor:
f(x)=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{ f'''(a)}{3!}(x-a)^3+...
Assim, podemos realizar as seguintes aproximações em torno de x=2:
\\\sqrt{x^2+12}= 4+\frac{1}{2}(x-2)+\frac{3}{32}(x-2)^2+...\approx 4+\frac{1}{2}(x-2)\\\\\sqrt{x^3-4}=2+3(x-2)-\frac{3}{4}(x-2)^2+...\approx 2+3(x-2)
Resolvendo o limite:
\\\lim_{x\to 2}\frac{\sqrt{x^2+12}-4}{2-\sqrt{x^3-4}}\approx\lim_{x\to 2}\frac{4+\frac{1}{2}(x-2)-4}{2-2-3(x-2)}\approx \boxed {-\frac{1}{6}}
Nota¹: para esta questão em específico talvez as Séries de Taylor não tenham o seu valor porque ficar derivando funções raiz é meio chato e sem contar que a resolução que o colega Emanuel postou é mais acessível. Porém, há alguns casos de limites trigonométricos, por exemplo, nos quais se torna bastante interessante a ideia de transformar uma função trigonométrica numa função polinomial pois facilita bastante a manipulação algébrica, o que facilita o cálculo do limite.
Nota²: eu parei a sequência na segunda parcela pois adiante dessa parcela todos os termos iria tender a zero quando x tendesse a 2.
Nota³: até onde eu sei não existe um igual entre o limite e a expressão que vem ao lado da simbologia de limite.
Nota4: para a=0 na série de Taylor encontra-se a Série de Maclaurin.
Assim, podemos realizar as seguintes aproximações em torno de x=2:
Resolvendo o limite:
Nota¹: para esta questão em específico talvez as Séries de Taylor não tenham o seu valor porque ficar derivando funções raiz é meio chato e sem contar que a resolução que o colega Emanuel postou é mais acessível. Porém, há alguns casos de limites trigonométricos, por exemplo, nos quais se torna bastante interessante a ideia de transformar uma função trigonométrica numa função polinomial pois facilita bastante a manipulação algébrica, o que facilita o cálculo do limite.
Nota²: eu parei a sequência na segunda parcela pois adiante dessa parcela todos os termos iria tender a zero quando x tendesse a 2.
Nota³: até onde eu sei não existe um igual entre o limite e a expressão que vem ao lado da simbologia de limite.
Nota4: para a=0 na série de Taylor encontra-se a Série de Maclaurin.
Última edição por Giovana Martins em Seg 13 Abr 2020, 03:04, editado 1 vez(es)

Giovana Martins- Grande Mestre

- Mensagens : 8563
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: limites de funções
Re: limites de funções
Giovana Martins escreveu:Um outro jeito por Séries de Taylor:f(x)=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+...
Assim, podemos realizar as seguintes aproximações em torno de x=2:\\\sqrt{x^2+12}= 4+\frac{1}{2}(x-2)+\frac{3}{32}(x-2)^2+...\approx 4+\frac{1}{2}(x-2)\\\\\sqrt{x^3-4}=2+3(x-2)-\frac{3}{4}(x-2)^2+...\approx 2+3(x-2)
Resolvendo o limite:\\\lim_{x\to 2}\frac{\sqrt{x^2+12}-4}{2-\sqrt{x^3-4}}\approx\lim_{x\to 2}\frac{4+\frac{1}{2}(x-2)-4}{2-2-3(x-2)}\approx \boxed {-\frac{1}{6}}
Nota¹: para esta questão em específico talvez as Séries de Taylor não tenham o seu valor porque ficar derivando funções raiz é meio chato e sem contar que a resolução que o colega Emanuel postou é mais acessível. Porém, há alguns casos de limites trigonométricos, por exemplo, nos quais se torna bastante interessante a ideia de transformar uma função trigonométrica numa função polinomial pois facilita bastante a manipulação algébrica, o que facilita o cálculo do limite.
Nota²: eu parei a sequência na segunda parcela pois adiante dessa parcela todos os termos iria tender a zero quando x tendesse a 2.
Nota³: até onde eu sei não existe um igual entre o limite e a expressão que vem ao lado da simbologia de limite.
Nota4: para a=0 na série de Taylor encontra-se a Série de Maclaurin.
Solução linda Giovana.
Essa nota³ me intriga bastante, eu tenho uma noção rasa de cálculo apenas para os livros de aprofundamento, não entendi bem, como assim o igual não existe ao lado do limite? Isso para todos os limites ou na série de Taylor?
____________________________________________
El Álgebra no es más que Geometría y la Geometría no es más que Álgebra abstracta
Sophie Germain
Sophie Germain
Emanuel Dias- Monitor

- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
 Re: limites de funções
Re: limites de funções
Obrigada, Emanuel.
Somos dois. O meu conhecimento de cálculo também é bem básico. Quanto ao que eu disse era o seguinte:
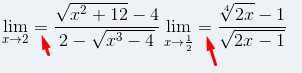
Tipo esse simbolo de igual entre a simbologia de limite e a função a qual quer se descobrir o limite não existe até onde eu sei. Pelo menos nunca vi nenhum livro adotando essa simbologia. E no caso isso é para todos os limites.
Somos dois. O meu conhecimento de cálculo também é bem básico. Quanto ao que eu disse era o seguinte:
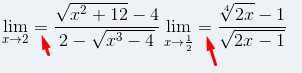
Tipo esse simbolo de igual entre a simbologia de limite e a função a qual quer se descobrir o limite não existe até onde eu sei. Pelo menos nunca vi nenhum livro adotando essa simbologia. E no caso isso é para todos os limites.

Giovana Martins- Grande Mestre

- Mensagens : 8563
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: limites de funções
Re: limites de funções
Giovana Martins escreveu:Obrigada, Emanuel.
Somos dois. O meu conhecimento de cálculo também é bem básico. Quanto ao que eu disse era o seguinte:
Tipo esse simbolo de igual entre a simbologia de limite e a função a qual quer se descobrir o limite não existe até onde eu sei. Pelo menos nunca vi nenhum livro adotando essa simbologia. E no caso isso é para todos os limites.
Ata, nossa eu nem tinha visto isso, com certeza isso não existe eu pensei que estava falando de algo tipo isso:
que susto kkk
____________________________________________
El Álgebra no es más que Geometría y la Geometría no es más que Álgebra abstracta
Sophie Germain
Sophie Germain
Emanuel Dias- Monitor

- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
 Re: limites de funções
Re: limites de funções
Atah kkkkkkkk. A propósito, a estrela ficou legal no perfil kkkkkk
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8563
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Página 1 de 2 • 1, 2 
 Tópicos semelhantes
Tópicos semelhantes» Limites de Funções
» Limites e Funções
» limites das funções
» Limites de funções
» Ajuda, funções e limites
» Limites e Funções
» limites das funções
» Limites de funções
» Ajuda, funções e limites
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos