Pontos Reais e Complexos e Área do Triângulo

Eu gostaria que, por favor, os colegas analisassem a solução que eu desenvolvi para a seguinte questão e dissessem se está correta ou não.

Enunciado: Calcule a área do triângulo cujos vértices são a origem e as interseções da hipérbole \frac{y^{2}}{9}-\frac{x^{2}}{2}=1 com a parábola y=x^{2}.


******************** MINHA SOLUÇÃO ********************

\left\{\begin{matrix}
\frac{y^{2}}{9} & - & \frac{x^{2}}{2} & = & 1\\
y & = & x^{2} &  &
\end{matrix}\right.

Resolvendo o sistema, temos: Y_{1}=6 ou Y_{2}=-\frac{3}{2}

Com isso temos: X_{1}=\pm\sqrt{6} ou X_{2}=\pm\frac{i\sqrt{6}}{2}

Devemos descartar o valor de X complexo. E assim os pontos que formam o triângulo são (0,0), (\sqrt{6},6),(-\sqrt{6},6).

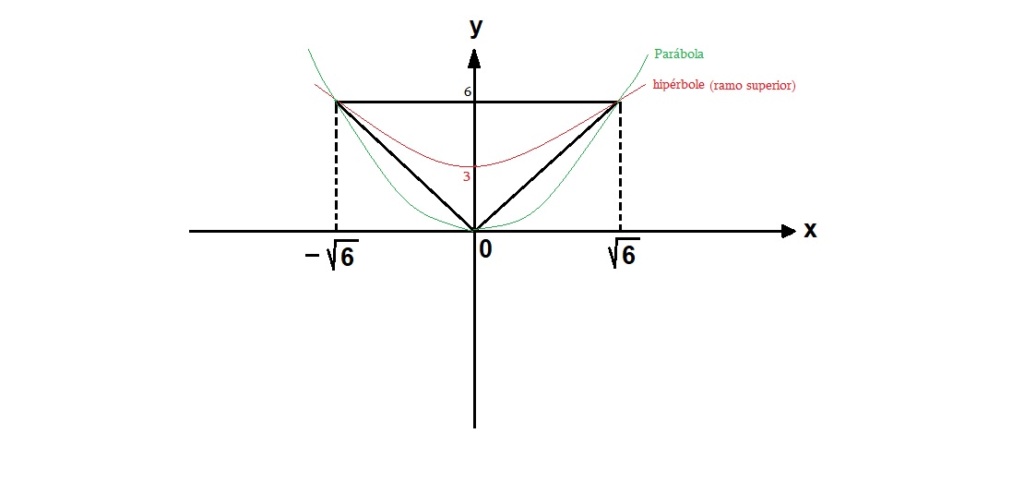
Assim temos a seguinte configuração:



E para calcular a área do triângulo basta fazermos o seguinte:

S_{T}=\frac{6\cdot(2\cdot\sqrt{6})}{2}=6\sqrt{6} u.a.

Eu aguardo a correção de um dos colegas.

Sua solução está correta.

As raízes x1 e x2 correspondem aos vértices da base e y corresponde à altura do triângulo, em relação à esta base: