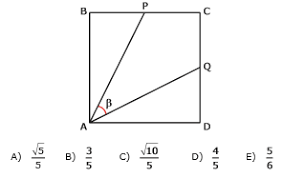
Quadrado
3 participantes
Página 1 de 1
Quadrado
por viniciuscz Qua 05 Fev 2020, 20:57
Seja ABCD um quadrado, e P e Q pontos médios de – BC e – CD, respectivamente. Então, sen β é igual a
Resposta: 3/5
Resposta: 3/5
Última edição por viniciuscz em Sex 07 Fev 2020, 22:03, editado 2 vez(es)
viniciuscz- Recebeu o sabre de luz
- Mensagens : 172
Data de inscrição : 04/05/2019
Idade : 23
Localização : Rondonópolis
Re: Quadrado
por Elcioschin Qua 05 Fev 2020, 21:16
Seja BP = CP = CQ = DQ = x ---> AB = AD = 2.x
Seja BÂP = DÂP = α
AP² = AB² + BP² ---> AP² = (2.x)² + x² ---> AP = x.√5
sen(BÂP) = BP/AB ---> senα = x/x.√5 ---> senα = √5/5 ---> cosα = 2.√5/5
cos(2.α) = 2.cos²α - 1 ---> cos(2.α) = 2.(4/5) - 1 ---> cos(2.α) = 3/5
β = 90º - 2.α ---> senβ = sen(90º - 2.α) ---> senβ = cos2.α ---> senβ = 3/5
Seja BÂP = DÂP = α
AP² = AB² + BP² ---> AP² = (2.x)² + x² ---> AP = x.√5
sen(BÂP) = BP/AB ---> senα = x/x.√5 ---> senα = √5/5 ---> cosα = 2.√5/5
cos(2.α) = 2.cos²α - 1 ---> cos(2.α) = 2.(4/5) - 1 ---> cos(2.α) = 3/5
β = 90º - 2.α ---> senβ = sen(90º - 2.α) ---> senβ = cos2.α ---> senβ = 3/5
Elcioschin- Grande Mestre
- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Quadrado
por viniciuscz Qua 05 Fev 2020, 21:31
não entendi essa parteElcioschin escreveu: cosα = 2.√5/5 --> cos(2.α) = 2.cos²α - 1 ---> cos(2.α) = 2.(4/5) - 1 ---> cos(2.α) = 3/5
β = 90º - 2.α ---> senβ = sen(90º - 2.α) ---> senβ = cos2.α ---> senβ = 3/5
viniciuscz- Recebeu o sabre de luz
- Mensagens : 172
Data de inscrição : 04/05/2019
Idade : 23
Localização : Rondonópolis
Re: Quadrado
por viniciuscz Qui 06 Fev 2020, 22:29
Que propriedade o senhor usou? como chegou a isso: cosα = 2.√5/5 --> cos(2.α) = 2.cos²α - 1
viniciuscz- Recebeu o sabre de luz
- Mensagens : 172
Data de inscrição : 04/05/2019
Idade : 23
Localização : Rondonópolis
Re: Quadrado
por Giovana Martins Qui 06 Fev 2020, 23:59
cos(a+b)=cos(a)cos(b)-sen(a)sen(b)
Se b=a: cos(2a)=cos(a)cos(a)-sen(a)sen(a)=cos²(a)-sen²(a)
Mas, sen²(a)=1-cos²(a), logo: cos(2a)=cos²(a)-[1-cos²(a)]=2cos²(a)-1
Para a linha seguinte: sen(β)=sen(90º-2α)=cos(2α) foi feito o seguinte:
sen(x-y)=sen(x)cos(y)-sen(y)cos(x)
sen(90°-2α)=sen(90°)cos(2α)-sen(2α)cos(90°), com cos(90°)=0, logo:
sen(90°-2α)=sen(90°)cos(2α)=1.cos(2α)=cos(2α)
Pesquise sobre identidades trigonométricas.
Algumas delas: http://paginas.unisul.br/eqm/download/trig/index.html
Se b=a: cos(2a)=cos(a)cos(a)-sen(a)sen(a)=cos²(a)-sen²(a)
Mas, sen²(a)=1-cos²(a), logo: cos(2a)=cos²(a)-[1-cos²(a)]=2cos²(a)-1
Para a linha seguinte: sen(β)=sen(90º-2α)=cos(2α) foi feito o seguinte:
sen(x-y)=sen(x)cos(y)-sen(y)cos(x)
sen(90°-2α)=sen(90°)cos(2α)-sen(2α)cos(90°), com cos(90°)=0, logo:
sen(90°-2α)=sen(90°)cos(2α)=1.cos(2α)=cos(2α)
Pesquise sobre identidades trigonométricas.
Algumas delas: http://paginas.unisul.br/eqm/download/trig/index.html
Giovana Martins- Grande Mestre
- Mensagens : 8563
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
viniciuscz- Recebeu o sabre de luz
- Mensagens : 172
Data de inscrição : 04/05/2019
Idade : 23
Localização : Rondonópolis
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
