Seletiva Cone Sul 2014 - Problema 3

No interior de um círculo unitário 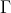 são marcados  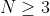segmentos de tal forma que a soma de todos esses  comprimentos é igual a 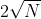. Prove que existe uma circunferência concêntrica a  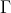que intersecta pelo menos dois desses segmentos.

Seja  s_i  o comprimento dos segmentos e fixe raio r. Seja os segmentos X_i  Y_i as  projeções circulares dos segmentos em  r  com x_i, y_i  as distâncias do centro aos pontos X_i  e  Y_i.

Se cada segmento é tangenciado por no máximo um dos círculos concêntricos, temos que
     
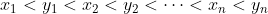                                                                    (1)

Não é difícil obter isso para cada  i, 

                                                                                  

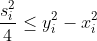
O segmento "existe" entre os círculos com raios  x_i  e  y_i. Adicionando da informação anterior, obtemos:

                                                                 

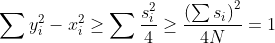
A última desigualdade é o trivial Cauchy-Schwarz. Agora, usando  (1)  e uma soma telescópica, obtemos:

                                                                      

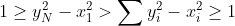
o que é uma contradição.