Seletiva Cone Sul 2000 - Problema 3
2 participantes
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Seletiva Cone Sul 2000 - Problema 3
por Time_Lady Dom 22 Dez 2019, 10:32
Se a, b, c são reais não nulos satisfazendo
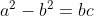e 
.
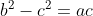Prove que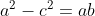
.
Prove que
Última edição por Time_Lady em Dom 22 Dez 2019, 19:16, editado 1 vez(es)
Time_Lady- Iniciante
- Mensagens : 3
Data de inscrição : 22/12/2019
Re: Seletiva Cone Sul 2000 - Problema 3
por NikolsLife Dom 22 Dez 2019, 17:27
Para começar, observe que, adicionando as duas equações dadas, podemos concluir imediatamente que
Agora, multiplique os dois lados por a - b, temos:
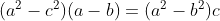
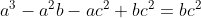
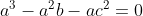
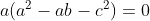
portanto, como a é diferente de 0, podemos concluir que a^2-ab-c^2 = 0, para que a ^ 2-c ^ 2 = ab, conforme desejado.
Agora, multiplique os dois lados por a - b, temos:
portanto, como a é diferente de 0, podemos concluir que a^2-ab-c^2 = 0, para que a ^ 2-c ^ 2 = ab, conforme desejado.
NikolsLife- Padawan
- Mensagens : 84
Data de inscrição : 10/12/2019
Tópicos semelhantes» Seletiva Cone Sul 2014 - Problema 3
» (Seletiva Brasileira Cone Sul - 2003)
» Cone - Fuvest 2000
» Problema com um cone
» Seletiva OBA 2016
» (Seletiva Brasileira Cone Sul - 2003)
» Cone - Fuvest 2000
» Problema com um cone
» Seletiva OBA 2016
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
