Função 2o grau Insper
4 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Função 2o grau Insper
Função 2o grau Insper
A figura representa os gráficos das funções quadráticas f(x) e g(x), ambas definidas de |R em |R. Uma das duas parábolas possui vértice V(0, 6) e a outra, vértice V’(–2, –6). Os pontos P, Q, R e S indicam as intersecções das parábolas com o eixo x, sendo que PR e QS são segmentos congruentes de medida igual a (2raiz de 6) unidades dos eixos
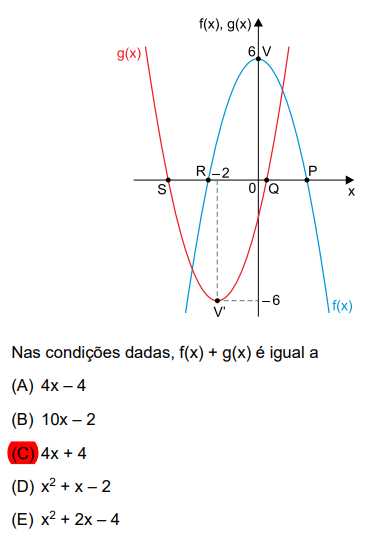
Estou com problemas em achar g(x). Usei Yv e Xv mas não achei pq faltou c. Com a distância, tentei x1+x2/2=Xv sendo x1+x2=-b/a mas não dá em lugar nenhum

- Spoiler:
- gab C.
Estou com problemas em achar g(x). Usei Yv e Xv mas não achei pq faltou c. Com a distância, tentei x1+x2/2=Xv sendo x1+x2=-b/a mas não dá em lugar nenhum
Última edição por raquelvaladao em Sex 10 Jan 2020, 09:19, editado 2 vez(es) (Motivo da edição : faltou um valor)

Raquel Valadão- Mestre Jedi

- Mensagens : 523
Data de inscrição : 04/04/2017
Localização : Bahia
 Re: Função 2o grau Insper
Re: Função 2o grau Insper
Sejam P(xP, 0), R(xR, 0), Q(xQ, 0), S(xS, 0)
Parábola azul:
xP = - xR
y = a.x² + b.x + c ---> b = 0 ---> c = 6 ---> y = a.x² + 6 ---> I
OP = OR = xP ---> II
P(xP, 0) ---> 0 - a.(xP)² + 6 ---> xP² = - 6/a ---> II
PR = 2.√6 ---> 2.xP = 2.√6 ---> xP = √6 ---> III
I ---> (xP)² = - 6/a ---> (√6)² = - 6/a ---> a = -1
Equação da parábola azul ---> y = - x² + 6 ---> IV
Parábola vermelha: y' = a'x² + b'x + c
V(-2, -6) ---> -6 = a1.(-2)² + b'(-2) + c' ---> - 2.a' + 2.b' = 6 - c' ---> V
QS = 2.√6 ---> xQ - xS = 2.√6 ---> VI
(xQ + xS)/2 = - 2 ---> xQ + xS = - 4 ---> VII
Parábola azul:
xP = - xR
y = a.x² + b.x + c ---> b = 0 ---> c = 6 ---> y = a.x² + 6 ---> I
OP = OR = xP ---> II
P(xP, 0) ---> 0 - a.(xP)² + 6 ---> xP² = - 6/a ---> II
PR = 2.√6 ---> 2.xP = 2.√6 ---> xP = √6 ---> III
I ---> (xP)² = - 6/a ---> (√6)² = - 6/a ---> a = -1
Equação da parábola azul ---> y = - x² + 6 ---> IV
Parábola vermelha: y' = a'x² + b'x + c
V(-2, -6) ---> -6 = a1.(-2)² + b'(-2) + c' ---> - 2.a' + 2.b' = 6 - c' ---> V
QS = 2.√6 ---> xQ - xS = 2.√6 ---> VI
(xQ + xS)/2 = - 2 ---> xQ + xS = - 4 ---> VII
Última edição por Elcioschin em Qui 09 Jan 2020, 22:43, editado 2 vez(es)

Elcioschin- Grande Mestre

- Mensagens : 73169
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Função 2o grau Insper
Re: Função 2o grau Insper
De onde a conclusao de que xP = xS? No lugar de xS não seria xR?Elcioschin escreveu:Sejam P(xP, 0), R(xR, 0), Q(xQ, 0), S(xS, 0)
Parábola azul:
xP = - xS
OP = OR = 2.xP ---> II
No lugar de 2 pq não 1? se é a metade?
Quanto a parabola vermelha, não consegui terminar a equação pra achar a função


Raquel Valadão- Mestre Jedi

- Mensagens : 523
Data de inscrição : 04/04/2017
Localização : Bahia
 Re: Função 2o grau Insper
Re: Função 2o grau Insper
f(x) = -x² + 6
Perceba que Xq - Xs = Xp - Xr = 2raiz de 6 (menos em vez de mais, pois está em módulo os números negativos)
e que seus vértices possuem a mesma ordenada y
Ambos possuem a mesma abertura, a diferença é que g(x) a abertura é positiva = 1.
Ai já da pra resolver XD
Perceba que Xq - Xs = Xp - Xr = 2raiz de 6 (menos em vez de mais, pois está em módulo os números negativos)
e que seus vértices possuem a mesma ordenada y
Ambos possuem a mesma abertura, a diferença é que g(x) a abertura é positiva = 1.
Ai já da pra resolver XD

Lucasdeltafisica- Jedi

- Mensagens : 484
Data de inscrição : 02/09/2017
Idade : 22
Localização : SSPSPSPSP
 Re: Função 2o grau Insper
Re: Função 2o grau Insper
Raquel
Você está certa: fiz as alterações em vermelho
Montei uma nova equação (em vermelho) para ajudar.
Você está certa: fiz as alterações em vermelho
Montei uma nova equação (em vermelho) para ajudar.

Elcioschin- Grande Mestre

- Mensagens : 73169
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Tópicos semelhantes
Tópicos semelhantes» (INSPER) Função do Segundo grau?
» Função trigonométrica Insper
» INSPER (2012) - Função Modular
» (Insper 2015) Q34 - Noções lógicas e função exponencial
» funcao do primeiro grau e segundo grau
» Função trigonométrica Insper
» INSPER (2012) - Função Modular
» (Insper 2015) Q34 - Noções lógicas e função exponencial
» funcao do primeiro grau e segundo grau
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













