Função trigonométrica Insper

por Raquel Valadão Qui 26 Mar 2020, 16:24

Insper) A figura mostra o gráfico da função f, dada pela lei:
f(x) = (senx + cosx)^4 – (senx – cosx)^4.

Spoiler:

Eu não tive nenhuma ideia melhor além de atribuir A pra cosx e B pra senx e abrir a equação chegando em f(x)=4sen^2a, mas isso não chega na resposta, então não entendi

por **Giovana Martins** Qui 26 Mar 2020, 16:55

Miga, nas duas primeiras linhas eu usei Prostaférese. Desconfio que haja uma resolução mais simples que esta. Vou tentar de outra forma. A propósito, eu não recomendo fazer substituições tipo A e B em equações trigonométricas porque ao fazer isso você perde de vista algumas simplificações que só dão certo na trigonometria.

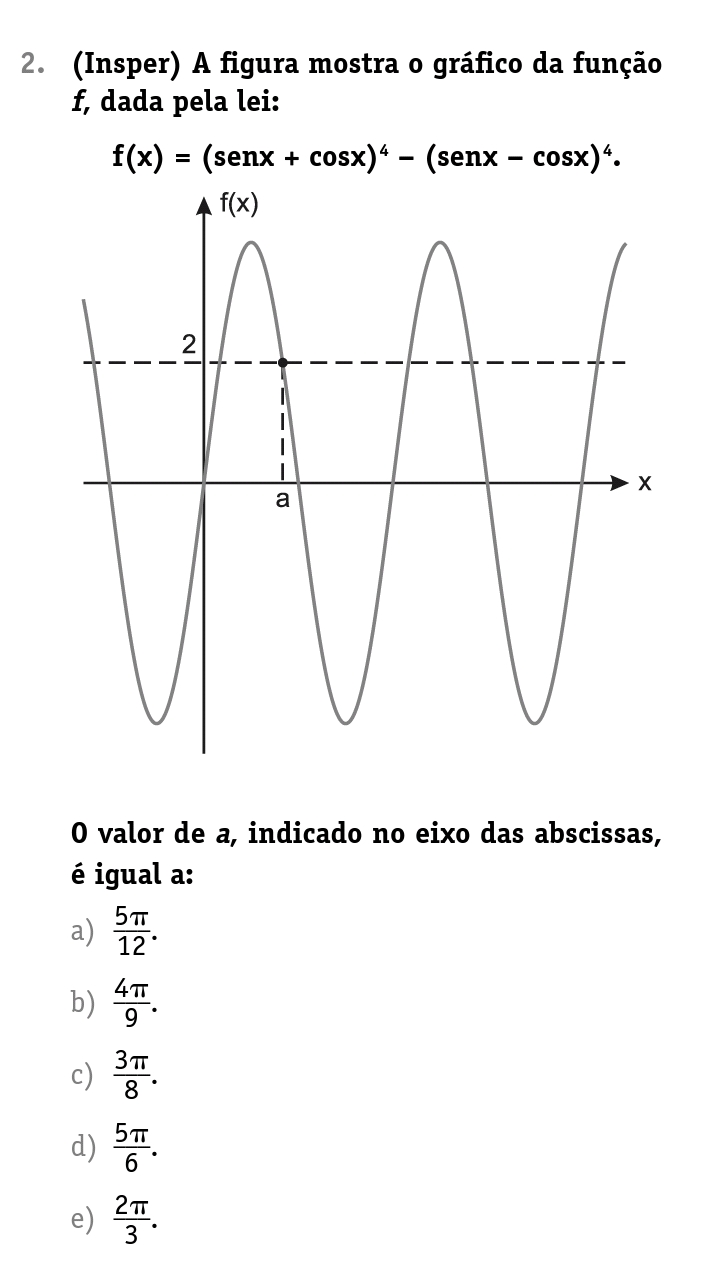
\\sen(x)+cos(x)=sen(x)+sen\left ( \frac{\pi }{2}-x \right )=\sqrt{2}cos\left ( x-\frac{\pi }{4} \right )\\\\sen(x)-cos(x)=sen(x)-sen\left ( \frac{\pi }{2}-x \right )=\sqrt{2}sen\left ( x-\frac{\pi }{4} \right )\\\\f(x)=[sen(x)+cos(x)]^4-[sen(x)-cos(x)]^4\\\\f(x)=4\left [cos^4\left ( x-\frac{\pi }{4} \right )-sen^{4}\left ( x-\frac{\pi }{4} \right ) \right ]\\\\f(x)=4\left [ cos^2\left ( x-\frac{\pi }{4} \right )-sen^2\left ( x-\frac{\pi }{4} \right ) \right ]\left [ cos^2\left ( x-\frac{\pi }{4} \right )+sen^2\left ( x-\frac{\pi }{4} \right ) \right ]\\\\f(x)=4\left [ 2cos^2\left ( x-\frac{\pi }{4} \right )-1 \right ]\ \therefore \ f(a)=2\ \to \boxed {a=\frac{5\pi }{12}}

por lejandrocohen Qui 26 Mar 2020, 16:59

Primeiro o produto notável-->

(a+b)^4= a^4+4a^3b+6a^2b^2+4ab^3+b^4
(a-b)^4= a^4-4a^3b+6a^2b^2-4ab^3+b^4

A=senx
B=cosx
F(x)=(sinx+cosx)^4-(sinx-cosx)^4

Substituindo e fazendo as subtrações: F(x)=8sinx^3cosx+8sinxcosx^3

Colocando em evidência(8sinxcox),ficará: F(x)=8sinxcosx(senx^2+cosx^2)

F(x)=8sinxcosx >>> F(x)=4 sen2x
Pedindo o que se pede,substituindo y por 2

2=4sen2a--> sen2a=1/2

perceba que pro sen ser 1/2,''a'' teria que ser 30,150....,porém tem 2 multiplicando,tendo assim que dividir esses números a metade no caso 15,75....

Logo, vejamos que o grafico tem vários pontos ''2'' logo, ''a'' é o segundo ponto,logo, a=75 ou 5pi/12

por Raquel Valadão Qui 26 Mar 2020, 17:23

Obrigada, pessoal!! Tinha esquecido das fórmulas de Prostaferese também.

Lejandro
Entao vou deixar escrito o mwu erro: confundi 2senxcosx com sen[size=38]²[/size]x, mas é sen2x, achando outro ângulo.

Giovana

Estou fugindo de equações trigonométricas igual o diabo foge da cruz.

por **Giovana Martins** Qui 26 Mar 2020, 17:31

"Giovana
Estou fugindo de equações trigonométricas igual o diabo foge da cruz."

kkkkk essa parte eu também considero bem difícil até pegar o jeito. É sempre bastante confuso mexer com equações trigonométricas.

Nota: guarde esta relação sen[(pi/2)-x] e as variações tipo cos[(pi/2)-x]. Elas junto com Prostaférese são bastante úteis em alguns casos. Infelizmente eu não sei nenhum esqueminha para decorar essas fórmulas. O jeito é deduzi-las. Pelo que eu me lembro as demonstrações delas são curtas.

por **Elcioschin** Qui 26 Mar 2020, 18:30

Raquel

Sua equação final está correta: f(x) = 4.sen(2.x)

O gráfico passa por (a, 2) ---> 2 = 4.sen(2.a) ---> sen(2.a) = 1/2

Na primeira volta temos duas soluções:

1) 2.a = pi/6 ---> a = pi/12 ---> não existe alternativa

2) 2.a = 5.pi/6 ---> a = 5.pi/12 ---> alternativa a)

Para outros usuários entenderem a sua solução;

f(x) = (senx + cosx)⁴ - (senx + cosx)⁴ --->

f(x) = [(senx + cosx)²]² - [(senx - cosx)²]²

f(x) = (sen²x + cos²x + 2.senx.cosx)² - (sen²x + cos²x - 2.senx.cosx)²

f(x) = [1 + sen(2.x)]² - [1 - sen(2.x)]² ---> a² - b² = (a + b).(a - b)

f(x) = [(1 + sen(2.x) + (1 - sen(2.x)].[(1 + sen(2.x) - (1 - sen(2.x)]

f(x) = 2.[2.sen(2.x)] ---> f(x) = 4.sen(2.x)