Probabilidade
3 participantes
Página 1 de 1
Probabilidade
por :Heisenberg.-. Seg 25 Nov 2019, 15:04
Dois dados idênticos, cujas faces são igualmente prováveis, têm a soma de suas faces opostas igual a sete. Se ao lançar simultaneamente os dois dados, ocorrer 4 em uma das faces laterais de um dado e 1 em uma das faces laterais do outro, qual é a probabilidade de a soma das faces voltadas para cima ser um número primo?
a)
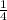
b)
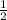
c)
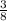
d)
e)
a)
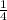
b)
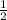
c)
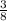
d)
e)
Última edição por :Heisenberg.-. em Ter 26 Nov 2019, 13:19, editado 1 vez(es)
:Heisenberg.-.- Jedi
- Mensagens : 200
Data de inscrição : 17/05/2019
Idade : 25
Localização : São Paulo
Re: Probabilidade
por Ashitaka Seg 25 Nov 2019, 16:28
Lateral 4 implica que a oposta é 3. Resta 1, 2, 5, 6.
Lateral 1 implica que a oposta é 6. Resta 2, 3, 4, 5.
Existem 4*4 = 16 combinações de pares: (1,2), (1,3), (1,4), ... etc.
As possíveis somas que resultam primos: (1, 2), (1,4), (2, 3), (2, 5), (5, 2), (6,5) ---->7 6 possibilidades.
Logo, 6/16 = 3/8.
edit: os pares estão corretos, mas contei 7 em vez de 6. Agora está arrumado.
Lateral 1 implica que a oposta é 6. Resta 2, 3, 4, 5.
Existem 4*4 = 16 combinações de pares: (1,2), (1,3), (1,4), ... etc.
As possíveis somas que resultam primos: (1, 2), (1,4), (2, 3), (2, 5), (5, 2), (6,5) ---->
Logo, 6/16 = 3/8.
edit: os pares estão corretos, mas contei 7 em vez de 6. Agora está arrumado.
Última edição por Ashitaka em Ter 26 Nov 2019, 16:14, editado 1 vez(es)
Ashitaka- Monitor
- Mensagens : 4365
Data de inscrição : 12/03/2013
Localização : São Paulo
Re: Probabilidade
por :Heisenberg.-. Ter 26 Nov 2019, 00:47
o gabarito é a C)Ashitaka escreveu:Lateral 4 implica que a oposta é 3. Resta 1, 2, 5, 6.
Lateral 1 implica que a oposta é 6. Resta 2, 3, 4, 5.
Existem 4*4 = 16 combinações de pares: (1,2), (1,3), (1,4), ... etc.
As possíveis somas que resultam primos: (1, 2), (1,4), (2, 3), (2, 5), (5, 2), (6,5) ----> 7 possibilidades.
Logo, 7/16.
:Heisenberg.-.- Jedi
- Mensagens : 200
Data de inscrição : 17/05/2019
Idade : 25
Localização : São Paulo
Re: Probabilidade
por Elcioschin Ter 26 Nov 2019, 11:48
Na realidade são 6 possibilidades das 16
1 + 2 = 3
1 + 3 = 4
1 + 4 = 5
1 + 5 = 6
2 + 2 = 4
2 + 3 = 5
2 + 4 = 6
2 + 5 = 7
5 + 2 = 7
5 + 3 = 8
5 + 4 = 9
5 + 5 = 10
6 + 2 = 8
6 + 3 = 9
6 + 4 = 10
6 + 5 = 11
p = 6/16 ---> p = 3/8
1 + 2 = 3
1 + 3 = 4
1 + 4 = 5
1 + 5 = 6
2 + 2 = 4
2 + 3 = 5
2 + 4 = 6
2 + 5 = 7
5 + 2 = 7
5 + 3 = 8
5 + 4 = 9
5 + 5 = 10
6 + 2 = 8
6 + 3 = 9
6 + 4 = 10
6 + 5 = 11
p = 6/16 ---> p = 3/8
Elcioschin- Grande Mestre
- Mensagens : 73176
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Probabilidade
por Ashitaka Ter 26 Nov 2019, 16:16
:Heisenberg.-. escreveu:o gabarito é a C)Ashitaka escreveu:Lateral 4 implica que a oposta é 3. Resta 1, 2, 5, 6.
Lateral 1 implica que a oposta é 6. Resta 2, 3, 4, 5.
Existem 4*4 = 16 combinações de pares: (1,2), (1,3), (1,4), ... etc.
As possíveis somas que resultam primos: (1, 2), (1,4), (2, 3), (2, 5), (5, 2), (6,5) ----> 7 possibilidades.
Logo, 7/16.
A resolução está correta, apenas o número de pares que somei como se fossem 7, embora houvesse, corretamente, escrito 6 pares. Uma leitura atenta revelaria isso.
Isso poderia ter sido evitado seguindo as regras do fórum:
XI- Não use letras maiúsculas para o título ou o corpo do texto da questão. Quando uma questão possui alternativas estas FAZEM PARTE da questão e devem ser postadas integralmente. Da mesma forma não deixe de postar a resposta esperada, se a conhecer. Isso será de valia para quem tentar ajudá-lo(a).
De nada, a propósito.
Ashitaka- Monitor
- Mensagens : 4365
Data de inscrição : 12/03/2013
Localização : São Paulo
Tópicos semelhantes» Probabilidade(Teorema da probabilidade total)
» Probabilidade - dobro da probabilidade
» Probabilidade
» Probabilidade
» Probabilidade [4]
» Probabilidade - dobro da probabilidade
» Probabilidade
» Probabilidade
» Probabilidade [4]
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
